- 目次
- 理解
- ICT
- 事例
- まとめ
【理解】正規分布の数学的解説
正規分布の定義について
$N(\mu, \sigma^2)$(正規分布)
ベルカーブ(正規分布のグラフ)
正規分布はガウス分布とも呼ばれ、グラフはベルカーブや釣鐘型と呼ばれる。


$N(0,1^2)$(標準正規分布)
$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx$(確率密度関数)
$\displaystyle F(x)= \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{x} e^{-\frac{(t-\mu)^2}{2\sigma^2}} dt$(累積分布関数)
$\displaystyle E \! \left[e^{tX}\right]
= \exp \! \left(\mu t + \tfrac{1}{2}\sigma^2 t^2\right)$(積率母関数)
正規分布の性質について
$X \sim N(\mu, \sigma^2)$ とする.
$E[X] =\mu$(平均値)
$V[X] = \sigma^2$(分散)
$\sigma[X] = \sigma$(標準偏差)
$X \sim N(\mu, \sigma^2)$, $a, b\in \mathbb{R}$ のとき $aX+b \sim N(a\mu+b, a^2\sigma^2)$(再生性)
$\displaystyle Z=\frac{X-\mu}{\sigma}$(標準化)
$X \sim N(\mu, \sigma^2)$ ならば, $Z \sim N(0,1^2)$ となる.
証明は, $\displaystyle a=\frac{1}{\sigma}$ と $\displaystyle b=-\frac{\mu}{\sigma}$ とすると, $Z=aX+b$ と表せることで上の再生性の証明に帰着することができる.
$X_1 \sim N(\mu_1, \sigma_1^2)$, $X_2 \sim N(\mu_2, \sigma_2^2)$ のとき $X_1+X_2 \sim N(\mu_1+\mu_2, \sigma_1^2 + \sigma_2^2)$(再生性)
$P(\mu -\sigma \leq X \leq \mu + \sigma) \fallingdotseq 0.68$,
$P(\mu -2\sigma \leq X \leq \mu + 2\sigma) \fallingdotseq 0.95$,
$P(\mu -3\sigma \leq X \leq \mu + 3\sigma) \fallingdotseq 0.99$
【ICT】正規分布の値を計算
【表計算】Excel・スプレッドシートで正規分布の計算
正規分布の累積積分関数NORM.DIST(x,mu,sigma,TRUE)
正規分布の確率密度関数NORM.DIST(x,mu,sigma,FALSE)
【コード】Pythonで正規分布の計算
正規分布の確率密度関数のグラフ scipy.stats.norm.pdf()
複数の正規分布の確率密度関数のグラフ scipy.stats.norm.pdf()
正規分布の累積分布関数のグラフ scipy.stats.norm.cdf()
正規分布の面積 $P(X \leq c)$ の図示 cdf(c, mu, sigma)
正規分布の面積 $P(c_1 \leq X \leq c_2)$ の図示 cdf(c2, mu, sigma)-cdf(c1, mu, sigma)
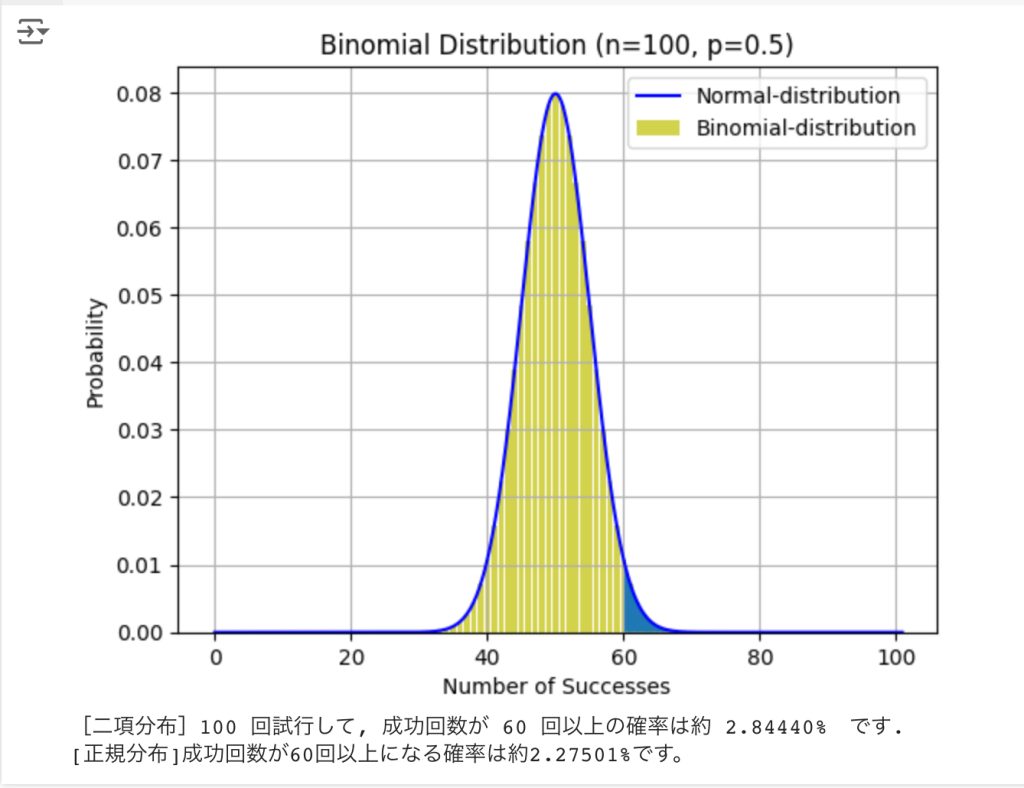
二項分布 $B(n,p)$ と正規分布 $N(np, np(1-p))$ の比較
【事例】正規分布の具体例
※ここは2学期に授業するので、今後早いうちに詳しく付け加えていきます。
偏差値(成績分布)
$N(50,10^2)$
パスタを半分に折る(誤差の分布)
パスタを半分に折る
(参考:青山学院大学寺尾先生HP)
人時計(誤差の分布)
心で数を数える
ゴルトンボード
【まとめ】ポイントノート
「正規分布」とは
実験や製造などの誤差がつくる自然な確率分布のこと。
確率密度関数
$\displaystyle f(x) = \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}}$($m \in \mathbb{R}$, $\sigma>0$)
A. 期待値 $E[X]$と分散 $V[X]$
正規分布に従う確率変数 $X$ について, $E[X] = m$, $V[X] = \sigma^2$.
記号
平均値 $m$, 標準偏差 $\sigma$ の
正規分布を $N(m, \sigma^2)$
と書く.
B. 正規分布の再帰性
独立な確率変数 $X$ と $Y$ が $N(m_1, \sigma_1^2)$ と $N(m_2, \sigma_2^2)$ にそれぞれ従うとき, $X + Y$ は正規分布 $N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)$ に従う.
C. 標準化(変数変換)
$N(m,\sigma^2)$ に従う確率変数 $X$ について, 確率変数 $\displaystyle Z=\frac{X-m}{\sigma}$ は 標準正規分布 $N(0,1^2)$ に従う.
D. 性質(確率の目安)
正規分布では, $m \pm 1\sigma$ では約$68 \%$, $m \pm 2\sigma$ では約$95 \%$, $m \pm 3\sigma$ では約$99 \%$の確率に対応する.
ポイント解説
正規分布は
ガウス分布
とも呼ばれ、グラフはベルカーブや釣鐘型と呼ばれる。


標準正規分布
$N(0,1^2)$ のこと:$$f(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{z^2}{2}}$$
確率密度関数の証明
$\int_{-\infty}^{\infty} f(x) dx=1$ であることは, ガウス積分 $\int_{-\infty}^{\infty} e^{-t^2} dx=\sqrt{\pi}$ より導かれる。
D
$m-n \sigma \leqq X \leqq m+n\sigma$ の範囲を $m \pm n \sigma$ と略記している。

EXCEL
NORM.DIST関数;引数には①データ範囲②平均値③標準偏差④関数形式(TRUE→下側累積確率, FALSE→確率密度関数の値)を入力する。