楕円の方程式の導出
公式（楕円）
中心が原点, $x$ 軸方向の半径の長さが $a>0$, $y$ 軸方向の半径の長さが $b>0$ の楕円の方程式は
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
である.
楕円の方程式を楕円の定義から導出してみよう。
例えば, $\displaystyle \frac{x^2}{25} + \frac{y^2}{9}=1$ は点 $(4, 0)$ と $(-4,0)$ が焦点の楕円を表す式です。方程式を満たす点 $(5,0)$ や点 $(0,3)$ への焦点からの距離の和は $10$ で一定です。
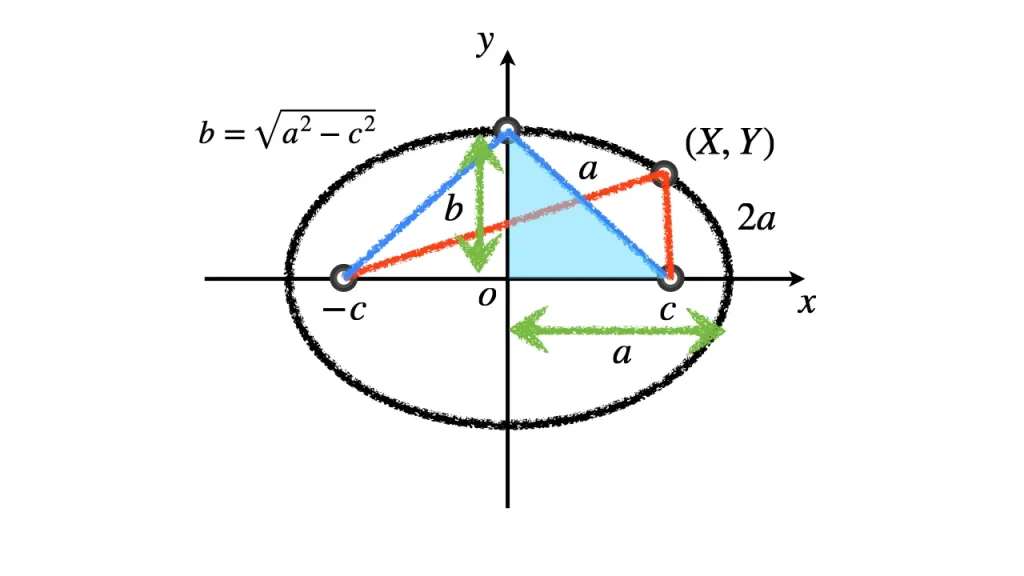
証明.
$c>0$ として, 座標平面上で焦点の座標を $\mathrm{F}(c, 0)$ と $\mathrm{F'}(-c, 0)$ とする.
焦点から楕円上の点 $\mathrm{P}(x,y)$ までのそれぞれの距離の和を $2a$ とすると, 点 $\mathrm{P}$ が
$$\displaystyle \mathrm{PF} + \mathrm{PF'} = 2a$$
を満たすことが楕円上の点である定義である.
楕円は焦点 $\mathrm{F}$ と $\mathrm{F'}$ からの距離の和が一定の点の集合である.
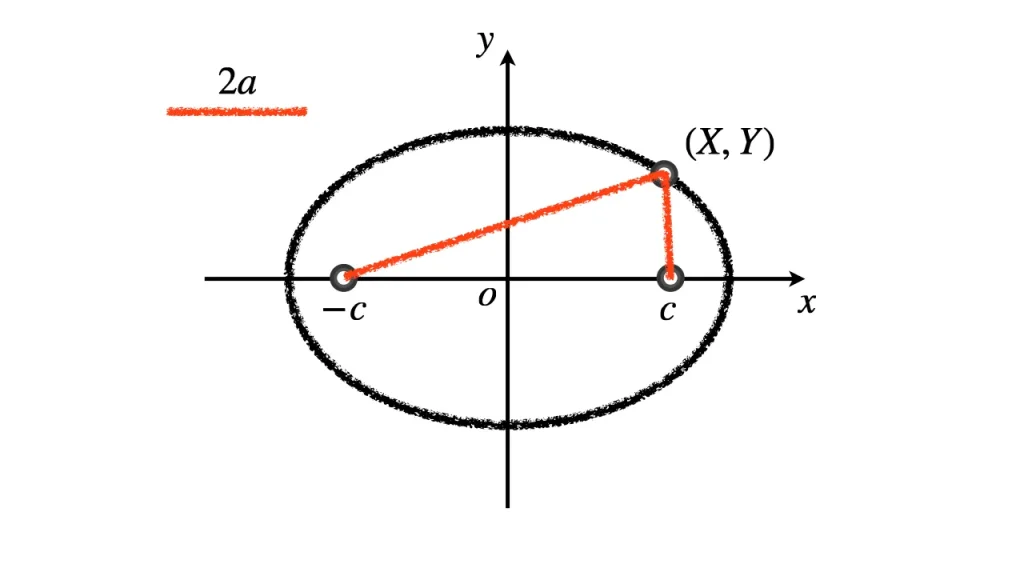
定義式を座標を使って書き換え計算する. $\mathrm{PF}$ と $\mathrm{PF'}$ は
$\displaystyle \mathrm{PF} = \sqrt{(x-c)^2 + y^2}$
$\displaystyle \mathrm{PF'} = \sqrt{(x-(-c))^2 + y^2}$
であり, 楕円の定義式から
$$\sqrt{(x-c)^2 + y^2} + \sqrt{(x-(-c))^2 + y^2} = 2a$$
を得る. 第2項目を右辺に移項し, 両辺を2乗すると
$\sqrt{(x-c)^2 + y^2} = 2a - \sqrt{(x-(-c))^2 + y^2}$
$(x-c)^2 + y^2 = 4a^2 - 4a \sqrt{(x+c)^2 + y^2} + (x+c)^2 + y^2$
となる. これを計算すると
$a \sqrt{(x+c)^2 + y^2} = a^2 + cx$
であり, 再度2乗すると
$(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$
となる. この式のグラフは $x$ 軸と $y$ 軸, 原点でそれぞれで対称であることが分かる.
$(x_0, y_0)$ が方程式を満たすとき, $(-x_0, y_0)$, $(x_0, -y_0)$, $(-x_0, -y_0)$ はすべて方程式を満たす.
定義で考えた $a$ が長軸半径に対応することを示す;
原点対称な楕円上の点のペアで, 最も距離が遠いときは, 2点ともが $x$ 軸上の対称な位置にあるときである.
このときのペアの点の間の距離は $2a$ である.
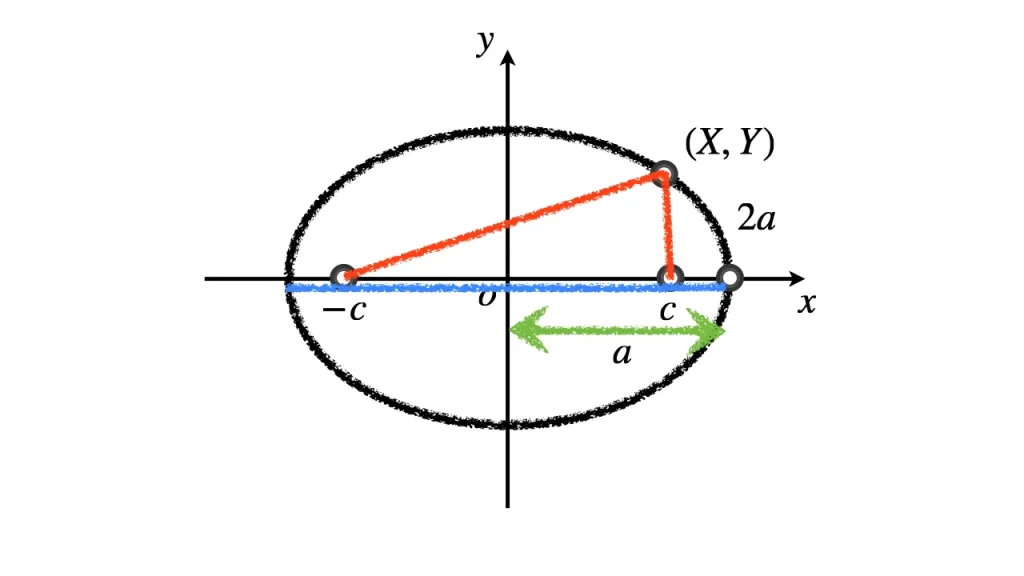
ゆえに, 定数 $a$ の値は楕円の長軸方向の半径の長さと一致する.
$\sqrt{a^2-c^2}$ が楕円の短軸半径であることを示す;
原点対称な楕円上の点のペアで, 最も距離が近いときは, 2点ともが $y$ 軸上の対称な位置にあるときである.
このときのペアの点の間の距離は $2\sqrt{a^2 - c^2}$ である.
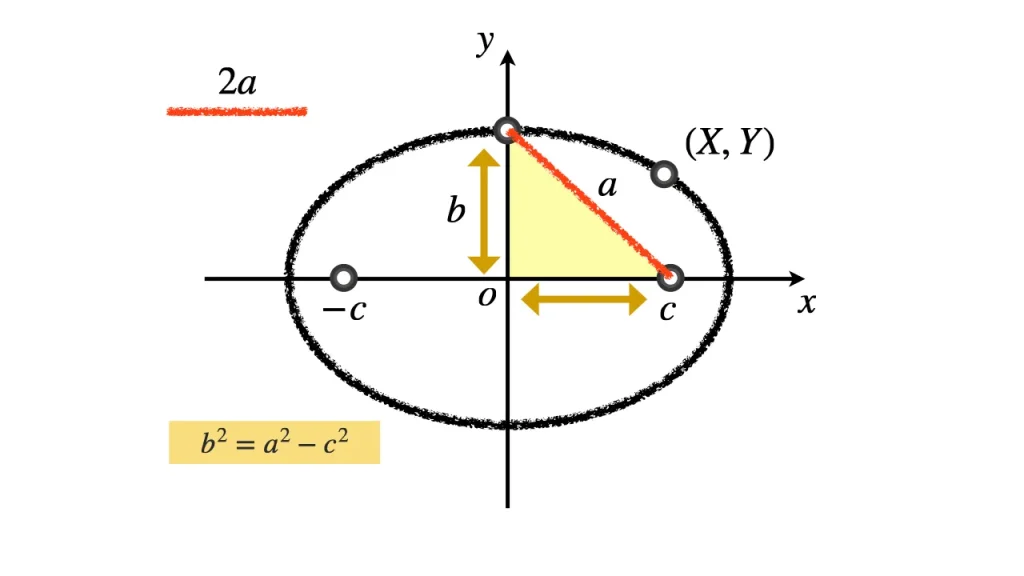
三平方の定理（図参照）より, 1つの点と原点の距離は $\sqrt{a^2-c^2}$ である.
ゆえに, $\sqrt{a^2 - c^2}$ が楕円の短軸半径の長さとなる. これを $b$ と置く.
さきほど計算した楕円の方程式
$$(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$$
について, $b^2 = a^2 - c^2$ と置きかえると
$$b^2 x^2 + a^2y^2 = a^2b^2$$
となり, 両辺を $a^2b^2>0$ で割ると
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
を得る.
ゆえに, 長軸半径 $a$, 短軸半径 $b$ の原点中心の楕円の方程式が上式で得られることが分かった.
