- 表紙
- まとめ
- コード
- 具体例
- 理解
数学のまとめノート
「正規分布」とは
実験や製造などの誤差がつくる自然な確率分布のこと。
確率密度関数
$\displaystyle f(x) = \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}}$($m \in \mathbb{R}$, $\sigma>0$)
A. 期待値 $E[X]$と分散 $V[X]$
正規分布に従う確率変数 $X$ について, $E[X] = m$, $V[X] = \sigma^2$.
記号
平均値 $m$, 標準偏差 $\sigma$ の
正規分布を $N(m, \sigma^2)$
と書く.
B. 正規分布の再帰性
独立な確率変数 $X$ と $Y$ が $N(m_1, \sigma_1^2)$ と $N(m_2, \sigma_2^2)$ にそれぞれ従うとき, $X + Y$ は正規分布 $N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)$ に従う.
C. 標準化(変数変換)
$N(m,\sigma^2)$ に従う確率変数 $X$ について, 確率変数 $\displaystyle Z=\frac{X-m}{\sigma}$ は 標準正規分布 $N(0,1^2)$ に従う.
D. 性質(確率の目安)
正規分布では, $m \pm 1\sigma$ では約$68 \%$, $m \pm 2\sigma$ では約$95 \%$, $m \pm 3\sigma$ では約$99 \%$の確率に対応する.
ポイント解説
正規分布は
ガウス分布
とも呼ばれ、グラフはベルカーブや釣鐘型と呼ばれる。


標準正規分布
$N(0,1^2)$ のこと:$$f(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{z^2}{2}}$$
確率密度関数の証明
$\int_{-\infty}^{\infty} f(x) dx=1$ であることは, ガウス積分 $\int_{-\infty}^{\infty} e^{-t^2} dx=\sqrt{\pi}$ より導かれる。
D
$m-n \sigma \leqq X \leqq m+n\sigma$ の範囲を $m \pm n \sigma$ と略記している。

EXCEL
NORM.DIST関数;引数には①データ範囲②平均値③標準偏差④関数形式(TRUE→下側累積確率, FALSE→確率密度関数の値)を入力する。
Pythonコード
試行回数を大きくしたとき二項分布は正規分布に近づいていくのか、Pythonでグラフを作成することで検証してみました。
二項分布のヒストグラムと正規分布のグラフを重ねて観察する実験①と、実際にどちらも確率を算出して確率が近似できているのかの実験②の2つを行っています。
目次
正規分布のコード【Python】
正規分布のPythonコード
次のコードをコピペすれば正規分布をPythonで描写できます。母平均と母標準偏差のところの数字を変えて、必要な正規分布を作成してください。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm #normは正規分布
mu = 50 # 母平均
sigma = 10 # 母標準偏差
#正規分布を表示
X = np.arange(mu-5*sigma, mu+5*sigma, 0.1)
Y = norm.pdf(X, mu, sigma)
plt.plot(X, Y, color="orange", label = "Normal-distribution")
#グラフの表示
plt.legend() #凡例表示
plt.show()正規分布の表示結果

【実験①】二項分布と正規分布の見た目の観察
実験開始(Pythonコード)
試行回数 $n$ の二項分布 $B(n, p)$ と正規分布 $N(np, np(1-p))$ の違いを観察するコードを紹介します。
今回のコードでは、二項分布 $B(100, 0.3)$ と 正規分布 $N(30, 21)$ を比較しています。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
from scipy.stats import norm
# 二項分布の情報
n = 100 # Number of trials
p = 0.3 # Probability of success
# Plot the binomial distribution
x_values = np.arange(0, n + 1)
binomial_probs = binom.pmf(x_values, n, p)
plt.bar(x_values, binomial_probs, color='y', alpha=0.7, label = "Binomial-distribution")
#正規分布を表示
mu = n*p # 母平均
sigma = np.sqrt(n*p*(1-p)) # 母標準偏差
X = np.arange(mu-3*sigma, mu+3*sigma, 0.1)
Y = norm.pdf(X, mu, sigma)
plt.plot(X, Y, color="b", label = "Normal-distribution")
# Other Informations
plt.legend() #凡例表示
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.title(f"Binomial Distribution (n={n}, p={p})")
plt.grid(True)
plt.show()試行結果
試行回数が $n=100$ のときと、他のいくつかの場合で二項分布のヒストグラムと、正規分布を重ねて描写しています。
$B(100, 0.3)$ と $N(30, 21)$ の比較

$n = 100$ のときは,二項分布(黄色)はかなり密なので,正規分布が近似になってそう。
$B(40, 0.3)$ と $N(12, 8.4)$ の比較

$n=40$ では,隙間が見えるが,まだ密なので良い感じで近似になってそう。
$B(30, 0.3)$ と $N(9, 6.3)$ の比較

$n=30$ のときも,まだ正規分布で近似できていると言ってもよさそう。
$B(10, 0.3)$ と $N(3, 2.1)$ の比較

$n=10$ のときは,二項分布の左右非対称性が目立つので,正規分布の対称性と相性が悪そう。
$B(5, 0.3)$ と $N(1.5, 1.05)$ の比較

$n=5$ では,だいぶ左右非対称のスカスカなので,近似の精度が良いのか?って思う。
以上から、試行回数が増えれば、二項分布と正規分布は一致していくと考えてもよさそうですね。
【実験②】二項分布と正規分布の確率の数値比較
二項分布で $P(a<X<b)$ の確率を計算したときと, 正規分布で $P(a<X<b)$ の計算をしたときの値の比較をして近似できているか調べたいと思いました。
実験開始(Pythonコード)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
from scipy.stats import norm
from scipy import stats
import math
# 試行回数と成功確率
n = 100 # 試行回数
p = 0.5 # 成功確率
A = 60 # [正規分布]A以上の所の確率を求める [二項分布]Aからnまでの確率の和を求める
# 二項分布を表示
x_values = np.arange(0, n)
binomial_probs = binom.pmf(x_values, n, p)
plt.bar(x_values, binomial_probs, color='y', alpha=0.7, label = "Binomial-distribution")
#正規分布を表示
mu = n*p # 母平均
sigma = np.sqrt(n*p*(1-p)) # 母標準偏差
X = np.arange(0, n+1, 0.1)
Y = norm.pdf(X, mu, sigma)
plt.plot(X, Y, color="b", label = "Normal-distribution")
# Other Informations
plt.legend() #凡例表示
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.title(f"Binomial Distribution (n={n}, p={p})")
plt.grid(True)
plt.fill_between(X[X >= A], Y[X >= A])
plt.show()
def sum_binomial_probs(n, p, m):
total_prob = 0.0
for k in range(math.ceil(m), n+1):
prob = binom.pmf(k, n, p) # 二項分布の確率質量関数を使用
total_prob += prob
return total_prob
sum_prob = sum_binomial_probs(n, p, A)
print(f"[二項分布]{n} 回試行して, 成功回数が {A} 回以上の確率は約{sum_prob*100: .5f}% です.")
probability = 1 - stats.norm.cdf(x = A, loc=mu, scale=sigma)
# 結果の表示
print(f"[正規分布]成功回数が{A}回以上になる確率は約{probability * 100:.5f}%です。")試行結果
実際に上のPythonコードを実行すると、次の出力が得られます。
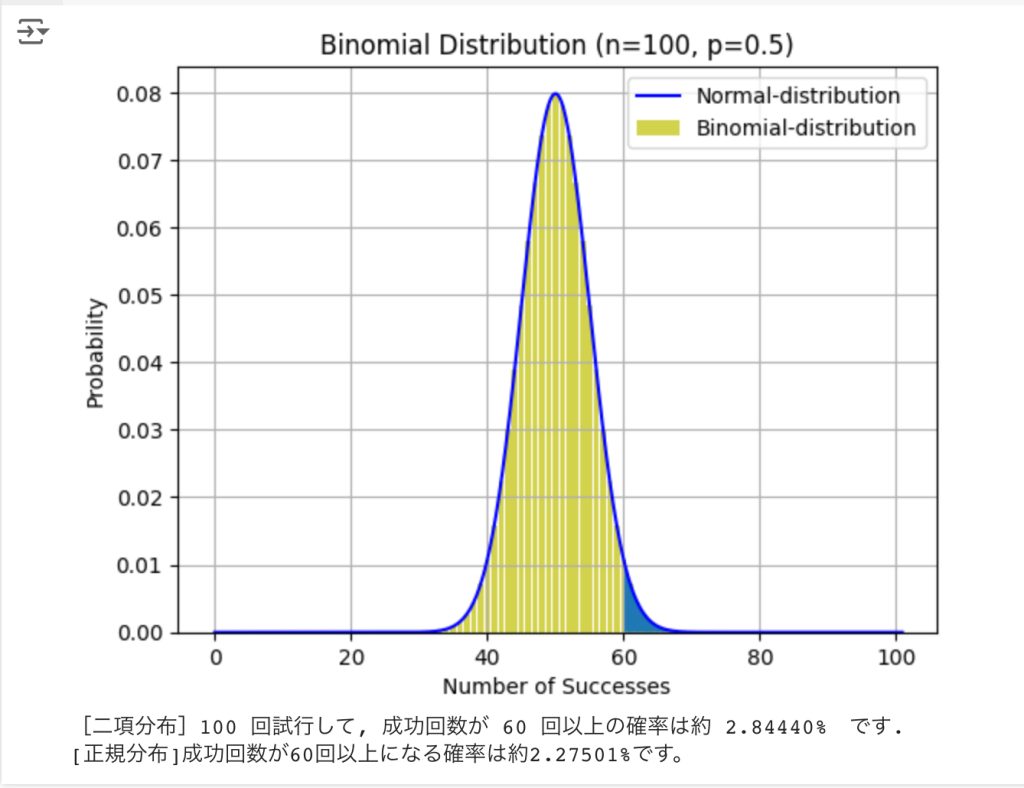
試行回数 $n=100$ のとき、成功回数が60回以上の確率を調べています。
黄色の二項分布の方は、約2.84%(0.0284)の確率で、青色の正規分布の方は約2.27%(0.0227)の確率でした。
「近似している」とは言えない感じですね。
「だいたい同じ」ということもできなくもないです。
でも、もっと試行回数が大きければ、もっと良い近似ができそうな気はします。
おおよその値を出すだけならば、どちらかの計算で代用しても良さそうです。
いろいろと数字を変えて、やってみてね!
確率密度関数の証明
正規分布の確率密度関数について証明で確かめることことが目標です。
命題. $m \in \mathbb{R}$, $\sigma>0$ としたとき, 次の関数 $f(x)$ は確率密度関数である.
$$\displaystyle f(x) = \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}}$$
この確率密度関数から定義される確率分布は正規分布 $N(m, \sigma^2)$ と記します。
正規分布の確率密度関数の証明
【前提】確率密度関数について
関数 $f(x)$ が確率密度関数であるとは、次の3条件を満たすことをいいます:
- $f(x) \geqq 0$
- $\displaystyle P(a \leqq X \leqq b) = \int_a^b f(x) dx$
- $\displaystyle \int_{-\infty}^{\infty} f(x) dx=1$
ここで $P$ は確率関数としています。
【仮定】ガウス積分について
今回は次の基本的なガウス積分の公式を仮定します。
補題(ガウス積分). $$\displaystyle \int_{-\infty}^{\infty} e^{-t^2} dx=\sqrt{\pi}$$
正規分布の確率密度関数の証明
下記の関数 $f(x)$ が確率密度関数であることを示します。
確率密度関数の定義の❶は自明です。定義の❷は、そのように確率 $P$ を定めればよいので、証明する必要はありません。
定義の❸にある、確率密度関数の積分が1であることを示しましょう。
証明すること→ $m \in \mathbb{R}$, $\sigma>0$のとき, 次の関数
$$\displaystyle f(x) = \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}}$$
について, $$\displaystyle \int_a^b f(x) dx=1$$ が成り立つことを示す.
証明.ガウス積分の等式を変数変換して, 証明することを示す.
被積分関数の変数変換
計算する積分 $$\displaystyle \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}} dx$$ について , $$\displaystyle t = \frac{x-m}{\sqrt{2}\sigma}$$ と変数変換をする. このとき, $-\infty < t < \infty$ であり, $dt = \displaystyle \frac{1}{\sqrt{2} \sigma}dx$ である.
ガウス積分に帰着する計算
変数変換をして計算をします;
$\begin{array}{ll}
\displaystyle \int_{-\infty}^{\infty} f(x) dx & \displaystyle = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}} dx \\
& \displaystyle = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}\sigma} e^{-\left( \frac{x-m}{\sqrt{2}\sigma} \right)^2} dx \\
& \displaystyle= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}\sigma} e^{-t^2}( \sqrt{2} \sigma) dt \\
& \displaystyle= \int_{-\infty}^{\infty} \frac{1}{\sqrt{\pi}} e^{-t^2}dt \\
& \displaystyle= \frac{1}{\sqrt{\pi}} \int_{-\infty}^{\infty} e^{-t^2}dt \\
& \displaystyle= \frac{1}{\sqrt{\pi}} \cdot \sqrt{\pi} \\
& = 1. \\
\end{array}$
以上で, 積分の値が $1$ であることが分かった. ■
このようにして、関数 $f(x)$ が確率密度関数だと証明できました。
この確率密度関数が作る確率分布が正規分布 $N(m, \sigma^2)$ です。



