- 目次
- 世の中
- 理解
- 表計算
- まとめ
【世の中】利子/金利・複利式とは
現代の金利事情
いまの金利が低すぎるので、銀行預金の金利を調べてみました。(2023年11月30日)
複利法の使いどころ
現代の金利事情(2023.11.30)
貯金、投資、保険、ローン、借金…
いま現在の銀行の「金利」は、どれくらいなのか調べてみました。
金利は「年利〇〇%」で表記することが通例のようです!

主要銀行の金利比較
すべて「通常貯金(普通預金)」に対する金利です。
※他の貯金の仕方だと"少し"金利が高い場合があります!
- ゆうちょ銀行→「0.001%」(金利一覧-ゆうちょ銀行)
- みずほ銀行→「0.001%」(預金金利・利率|みずほ銀行)
- UFJ銀行→「0.0010%」(円預金金利|三菱UFJ銀行)
- 三井住友銀行→「0.001%」(円預金金利:三井住友銀行)
- りそな銀行→「0.001%」(円預金金利|口座を開きたい|りそな銀行)
※すべて2023年11月30日現在の情報*
Wow!!ぜんぶ金利低すぎるorz
不景気ですね。
もう少し銀行の金利比較
バブルの頃は、定期預金が年利5%を越えていたようです。(今の時代では信じられないですね!)
- PayPay銀行→残高100万円未満「0.001%」, 残高100万円以上「0.001%」(円預金金利・預金金利-PayPay銀行)
- 楽天銀行→「0.02%」(定期預金や外貨預金の預金金利|楽天銀行)
※すべて2023年11月30日現在の情報*
通常貯金ではなく、「定期預金」をザッと見ると、「0.002%」の金利でした。
積立貯金をするときの複利
まず,複利の計算に必要な情報を整理する。
毎年同じ金額を積み立てて預金したとき、○○年後には預金額(元利合計額)はいくらになっているか?
次の表の情報から、未来の元利合計額が算出する。
| 意味 | 例(預金) | 例(借金) | 文字 |
|---|---|---|---|
| 発生額(&積立額) | 10万円 | 50万円 | $a$ |
| 利率 | 0.01(1%) | 0.1(10%) | $r$ |
| $1 + r$ | 1.01 | 1.1 | $b$ |
| 何年後か? | 30年後 | 30年後 | $n$ |
金利の付け方の整理
単利法
単利法は自分が預けたお金(預金額-元金)にしか「利子」が付きません。
国債などの金利は、単利だそうです。
複利法
複利法は、自分が預けたお金と、得た利子に対しても、さらに「利子」がつきます。
銀行の預金などの金利は、複利だそうです。
単利と複利の違い
単利と複利の言葉だけ聞いていても、単利と複利の違いがあまり判りません。
■単利の計算例
〜例えば(金利10%で100万円預けた場合)〜
100万円預けた場合
→1年後の利子(1,000,000×0.1)→利子「10万円」です。
→2年後の利子→変わらず利子「10万円」です。
■複利の計算例
〜例えば(金利10%で100万円預けた場合)〜
→1年後の利子(1,000,000×0.1)→利子「10万円」です。
→2年後の利子(1,100,000×0.1)→変わらず利子「11万円」です。
※単利も複利も説明を容易にするために、利子を高めの10%にしました。
計算するときは「10%=0.1」にしてくださいね!
ちなみに「0.001%」というのは、計算の際は「0.00001」にします。
かなり低い数値ですね。
いま「10%」という幻の金利で計算しました。
「1年で1万円」の差がでました。
しかし、単利と複利は、長期的に見た方が、その違いが非常に顕著に見えます。

アインシュタインの名言(複利の不思議)
Compound interest is the 8th wonder of the world.
Albert Einstein
He who understands it, earns it… he who doesn't…pays it.
JackとJillの物語(年利10%)
【弟のジャック】姉のジルと遊んでいる最中に頭をケガしてしまい、大学に進学できませんでした。18歳から働き始めて、毎月4万円ずつ8年間だけ積立投資をしました。その後はお金を積み立てせずに、投資金額の累計は384万円(毎月4万円 × 12カ月 × 8年)のまま65歳まで運用を続けました。
【姉のジル】弟のジャックと遊んでいたときの罪の意識もあり、医大に進学しました。26歳で働き始めて、毎月4万円ずつ65歳までの40年間積立投資をしました。結果、ジルの投資金額の累計は1,920万円(毎月4万円 × 12カ月 × 40年)です。
【引用】
①リック・イーデルマン, 家庭の金銭学, きんざい
②リベラルアーツ大学, 【薬が毒に?】複利のすごさが分かるエピソードと複利が壊す「生きるセンス」3つを解説, 2024.10.24アクセス
$72$ の法則
複利で資産を2倍にするために必要な期間の簡単な計算式のこと
$72 \div (\textrm{利率}[\%])$ $=\textrm{(2倍にするために必要な複利の回数)}$
[例]年利率 $3 \%$ ならば, $72 \div 3 = 24$ 年かかる。
【理解】複利式の数学的な解説
初期投資額 $a$ 円 とする。複利式での利子率を $r$ とします。複利式で $n$ 回の利子を受け取った後の元利合計を $a_n$ 円とします。
初期投資のみ(預けっぱなし)の場合
$a_n = a(1+r)^n$
複利式での資金の変化を考えてみよう。例えば, 利率が $10\%$ で $10$ (万)円を投資した場合, $n$ 年後には $10 \times (1.1)^n$ 万円になります。
基本の解法
利子率 $r$, 投資額 $a$とする。複利式で $n$ 回の利子を受け取った後の元利合計 $a_n$ は次の通り: $$a_n = a (1+r)^n$$
$n$ 回で受け取った利子の合計は $a(1+r)^n - a$ である。
複利式は、ある年度に受け取った利子にも、その次年度に利子が付くという方式である。
年利で考えると(次年度の利子)=(今年度までの元利合計)×(利率)である。
これより(次年度の元利合計)=(今年度までの元利合計)×(1+利率)が成り立つ。
例題. 複利の利子率が $10\%$, 初回の投資額を $10$ (万)円 とする。$10$ 回目の利子を受け取った後の元利合計および利子はいくらか。
与えられた条件から $n$ 回目の利子を得た後の元利合計を $a_n$ とすると $a_n = 10 \times (1.1)^n$ (万) である。
$r = 0.1$, $a = 10$(万).
$n=10$ のとき $a_{10} = 10 \times (1.1)^{10}\fallingdotseq 25.9374$ である。
ゆえに, 10回目の利子を受け取った後の元利合計は 259,374円である。
投資金額は 10万円であるので、受け取った利子は $25.9374-10$ $=15.9374$ (万) である。
ゆえに10回で受け取った利子の総額は 159,374円である。
単利式の場合, 10回で受け取る利子の総額は 10万円である。
複利の利子率が $10\%$, 投資額を $10$ (万)円 とします。単位は(万)として年利で考えます。
1年後の利子は $10 \times 0.1$ です。
1年後の元金と利子の合計は: $10 \times (1+0.1)$ $= 10 \times 1.1$.
2年後の利子は $(10 \times 1.1) \times 0.1$ です。
2年後の元金と利子の合計は: $(10 \times 1.1) \times (1 + 0.1)$ $= 10 \times (1.1)^2$.
3年後の利子は $(10 \times (1.1)^2) \times 0.1$ です。
3年後の元金と利子の合計は: $(10 \times (1.1)^2) \times (1+0.1)$ $= 10 \times (1.1)^3$.
この規則で $n$ 年後の元利合計が分かりますね!
毎回同額積立( $a$ 円ずつ )の場合
$\displaystyle a_n=\frac{a}{r}\{ (1+r)^{n+1} -1 \}$
複利式で、毎回同額ずつを積み立てた場合の資金の変化を考えてみよう。
例えば, 年利率が $0.1(10\%)$ で $10$ (万)円を毎年積み立てた場合, $n$ 年後には $$\frac{10 \{ (1.1)^{n+1} -1\}}{0.1} \text{(万)円}$$になります。
基本の解法
利子率 $r$, 毎回の積立額 $a$ とする。複利式で $n$ 回の利子を受け取った後の元利合計は次の通り:
$\displaystyle \sum_{k=0}^n a (1+r)^k$ $\displaystyle = \frac{a}{r} \{(1+r)^{n+1} - 1 \}$
ただし, $n$ 回目の利子を受け取った回に積み立てた額も含む。
証明.
$0 \leqq k \leqq n$ とする。初回から数えて$n$ 回目の利子を受け取るとき時点では, $k$ 回目に積み立てた額 $a$ には 利子を $n-k$ 回付くため元利合計は $a(1+r)^{n-k}$ となる。
$k=0$ のときは初回に投資した $a$ を指す。初回から数えて $n$ 回目の利子を受け取る時点では, 利子が $n$ 回すべて付くため, 元利合計は $a(1+r)^{n-0} =a(1+r)^n$ となる。
$k=n$ のときは $n$ 回目の利子を受け取った時点での積立額を指す。これに利子は未だ付かないので, 元利合計は元金のままで $a(1+r)^{n-n} =a$ となる。
$n$ 回目の利子を受け取る時点での元利合計の総額は, 各回の積立額に利子が付いた額の和である。したがって, $$\sum_{k=0}^n a (1+r)^{n-k}$$ が求めるものである。
$\displaystyle \sum_{k=0}^n a (1+r)^{n-k}$ $= a(1+r)^n + \cdots + a(1+r) +a$.
$\{ a (1+r)^{n-k} \}_{0 \leqq k \leqq n}$ は等比数列である。また, $\{ a (1+r)^{k} \}_{0 \leqq k \leqq n}$ は項を足す順番を逆にした数列で初項 $a$, 公比 $1+r$ の等比数列である。等比数列の和の公式より
$\begin{aligned}
&\sum_{k=0}^n a (1+r)^{n-k} \\
&= \sum_{k=0}^n a (1+r)^{k} \\
&= \frac{a \{ (1+r)^{n+1} - 1 \}}{(1+r) - 1} \\
&= \frac{a}{r} \{ (1+r)^{n+1} - 1 \}.
\end{aligned}$
初項 $a$, 公比 $R$ の等比数列の和の公式は次の通り: $$\sum_{k=0}^n a R^{k} = \frac{a(R^{n+1} -1)}{R-1}$$
ゆえに, $n$ 回目の利子を受け取った後の積立の元利合計の総額は $$\frac{a}{r} \{ (1+r)^{n+1} - 1 \}$$ である。
複利の年利率が $0.1$ $(10\%)$, 投資額を $10$ (万)円 とします。
各年度で投資した $10$ 万円の10年間の推移を表にしました。
| 積立年度 | 投資額 | 利子を含めた10年後の金額 |
|---|---|---|
| 初年度 | 10万円 | $10(1.1)^{10}$ 万円 |
| 1年後 | 10万円 | $10(1.1)^{9}$ 万円 |
| 2年後 | 10万円 | $10(1.1)^{8}$ 万円 |
| $\vdots$ | $\vdots$ | $\vdots$ |
| 9年後 | 10万円 | $10 \times (1.1)$ 万円 |
| 10年後 | 10万円 | $10$ 万円 |
| 合計額 | 110万円 | $185.311$ 万円 |
10年後の元利合計の総額は
$10(1.1)^{10}$ $+10(1.1)^{9}$ $+10(1.1)^{8}$ $+ \cdots$ $+10 \cdot (1.1)$ $+10$
です!
毎回同額積立( $a$ 円ずつ )の場合
$a_{n+1} = (1+r)a_n + a$
→ $\displaystyle a_n=\left(a_1 + \frac{a}{r} \right) (1+r)^n - \frac{a}{r}$
複利で毎回同額の積立をする場合の漸化式 $a_{n+1} = (1+r)a_{n} + a$ と一般項を扱ってみよう。
複利式の漸化式
利子率 $r$, 毎回の積立額 $a$ とする. $a_n$ を $n$ 回目の利子を受け取った後の元利合計とする. $$a_{n+1} = (1+r)a_n + a.$$
複利式積立の公式
利子率 $r$, 毎回の積立額 $a$ とする. 初回の投資額を $a_1$ とする. $n$ 回目の利子を受け取った後の元利合計: $$\left(a_1 + \frac{a}{r} \right)(1+r)^n - \frac{a}{r}$$
ただし, $n$ 回目の利子を受け取った回に積み立てた額も含む。
※ 利子率が $r$ で, $n$ 回目の利子を受け取りその回の積立額 $a$ も含めた元利総額を $a_n$ としています。
複利式で年利積立の場合の条件式は(次年度の残高)=(今年度の残高)×(1+利率) + (積立金)である。
初回の元金を $a_0$ とする。$n$ 年目の残高を $a_n$ とすると $a_{n+1}$ $= (1+r)a_n + a$ となる。
[基本の解法]積立額(複利式)の漸化式 $a_{n+1} = (1+r)a_{n} + a$ から一般項を導く解法は $a_{n+1} = pa_n +q (p \neq 1)$ の形の漸化式から一般項を導く方法を利用する。
例題. 複利の利子率が $10\%$, 毎回の積立額が $10$ (万)円, 初回の投資額を $50$ (万)円 とする。$n$ 回目の利子を受け取った後の資産はいくらか。
与えられた条件から $n$ 年目の資産 $a_n$ が満たす漸化式は $a_{n+1} = 1.1 a_n + 10$, $a_0 = 50$ とできる。
$r = 0.1$, $a = 10$(万), $a_1 = 50$(万).
この漸化式は $a_{n+1} +100 = 1.1(a_n + 100)$ と変形できる。
$a_{n+1} = pa_n +q$ は $x = px+q$ を満たす $x$ を用いて, $a_{n+1} - x = p(a_n -x)$ と変形できる。
$\displaystyle x = -\frac{a}{r}$ は積立額を利率で割った値のマイナスを付けたもの.
$\{ a_n + 100 \}_n$ という数列は公比 $1.1$ の等比数列である。また, 初項は $a_0+100 = 50+100 = 150$ である。ゆえに, $a_n + 100 = 150 (1.1)^n$ とできる。
$b_n = a_n+100$ と置くと, $b_{n+1} = a_{n+1} + 100$ である。$a_{n+1} +100 = 1.1(a_n +100)$ は $b_{n+1} = 1.1 \cdot b_n$ となる。
以上から $$a_n = 150 (1.1)^n-100$$ を得る。
複利の利子率が $10\%$ $(r=0.1)$, 毎回の積立額が $10$ (万)円, 初回の投資額を $50$ (万)円 とする。
$n$ 回目の利子を受け取った後の資産の定義式は
$a_{n+1}$ $= (1+0.1)a_n + 10$
となる。この数列の一般項を導くと
$a_n$ $= 150 (1.1)^{n}-100$
になる:
動画による解説
積立の場合(解説動画)
10秒チェックテスト
【表計算】Excelで複利式をシミュレーション
30年後の預金額のシミュレーション
$n$ 年後の残高(元利合計額)の自動算出
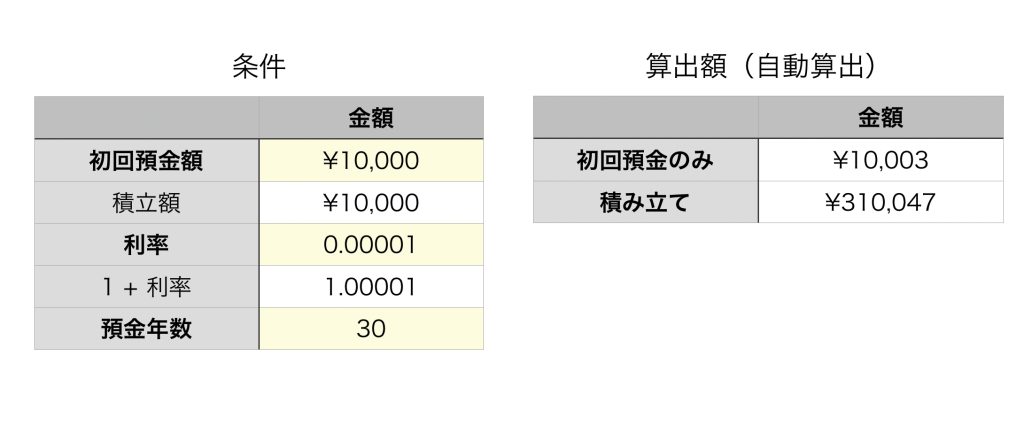
Excel・Numbers(表計算ソフト)で30年後の複利の結果をシミュレーションして計算しました!
もう少し簡単なシミュレーションはこちらで紹介しています。
複利シミュレーション(積立額の自動算出)
複利シミュレーションのテーマ(状況)
A銀行の年利が複利式で「0.001%」でした。
あなたのお年玉を銀行に預けました。
30年後に預金を引き出すとすると、いくらになっているでしょうか?
表計算ソフト

Numbersで解説しますが、ExcelもしくはGoogleスプレッドシートでも同様に作成可能です。
NumbersはiPhoneでもできます!
複利シミュレーションの完成イメージ
次のようなシミュレーションシステムを作ります。

『左側の条件の表(の黄色のトコロ)に必要事項を入力すると、
右側に自動的に未来の預金額が算出できるシステム』です!
今の画面は,次の条件で複利を計算しています;
例えば、預けるのを10万円の定期預金に替えて、利率を0.002%に変更します。
黄色いところだけ変更します。

簡単に30年後の預金額が算出できました♪( ´▽`)パチパチ
複利シミュレーションの作成手順
STEP①
Numbersに次のように打ち込んでください。そのまま同じように打ち込みます。

Numbersの機能
なお、Numbersでは図のように同じシートに表を2つ並べることができます。
下の図のようにやってください。
※ExcelやGoogleスプレッドシートではできません。
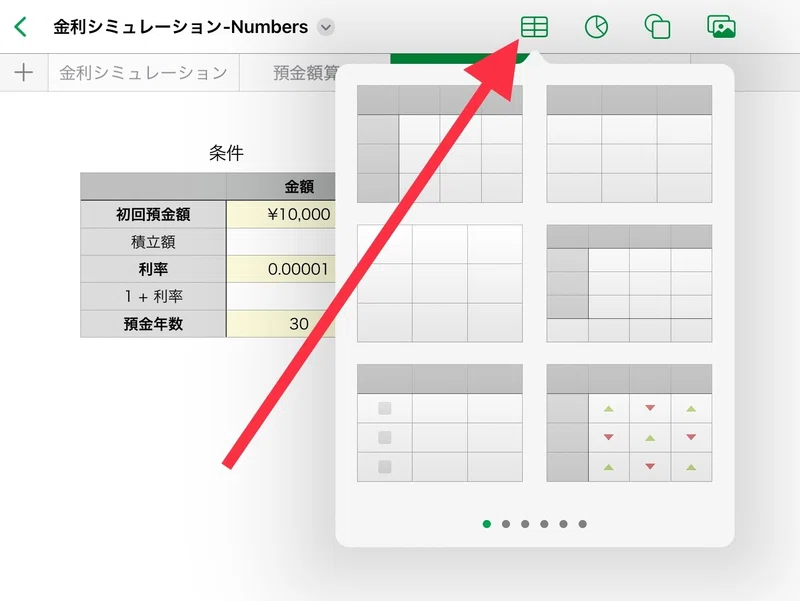
STEP②
[積立額の金額]のところをクリックします。
- 「=」を入力します。
- 「初回預金額の金額の¥10,000」のところをクリックします。
- [Enter]を押します。

で、OKです。
STEP③
数式の $b$ に対応する数値を入力します。
[1+利率 の 金額]のところをクリックします。
- 「=」を入力します。
- 「1 + 」と入力します。
- 「利率の0.00001」のところをクリックします。
- [Enter]を押します。

STEP④
預けて寝かすタイプの数式の $a(a+r)^n$ を利用します。
[初回預金の金額]のところをクリックします。
- 「=」を入力します。
- 「初回預金額の¥10,000」をクリック
- 「× (1+」と入力
- 「利率の0.00001」をクリック
- 「)^」と入力
- 「預金年数の30」をクリック
- [Enter]を押します。

STEP⑤
積立タイプの場合の $\displaystyle \frac{a(b^n-1)}{b-1}$ を利用します。
[積み立ての金額]のところをクリックします。
- 「=」を入力します。
- 「初回預金額の¥10,000」をクリック
- 「× (」と入力
- 「1+利率の1.00001」をクリック
- 「)^(」と入力
- 「預金年数の30」をクリック
- 「+1) - 1)/」と入力 ※「÷」の記号は「/」スラッシュ
- 「利率の0.00001」をクリック
- [Enter]を押します。

で、OKです。
あとは、黄色の数値を自分のシミュレーションしたい値に換えて楽しんでみてください!( ◠‿◠ )
残高(元利合計額)の推移グラフ

Excel・Numbers(表計算ソフト)で30年後の複利の結果をシミュレーションして計算しました!
もう少し数学の計算を踏まえたシミュレーションはこちらで紹介しています。
複利シミュレーション(推移グラフ)
複利シミュレーションのテーマ(状況)
A銀行の年利が複利式で「0.001%」でした。
あなたのお年玉を銀行に預けました。
30年後に預金を引き出すとすると、いくらになっているでしょうか?
複利法の数学の公式を知らなくてもシミュレーションできます。
表計算ソフト

Numbersで解説しますが、ExcelもしくはGoogleスプレッドシートでも同様に作成可能です。
NumbersはiPhoneでもできます!
複利シミュレーションの作成手順
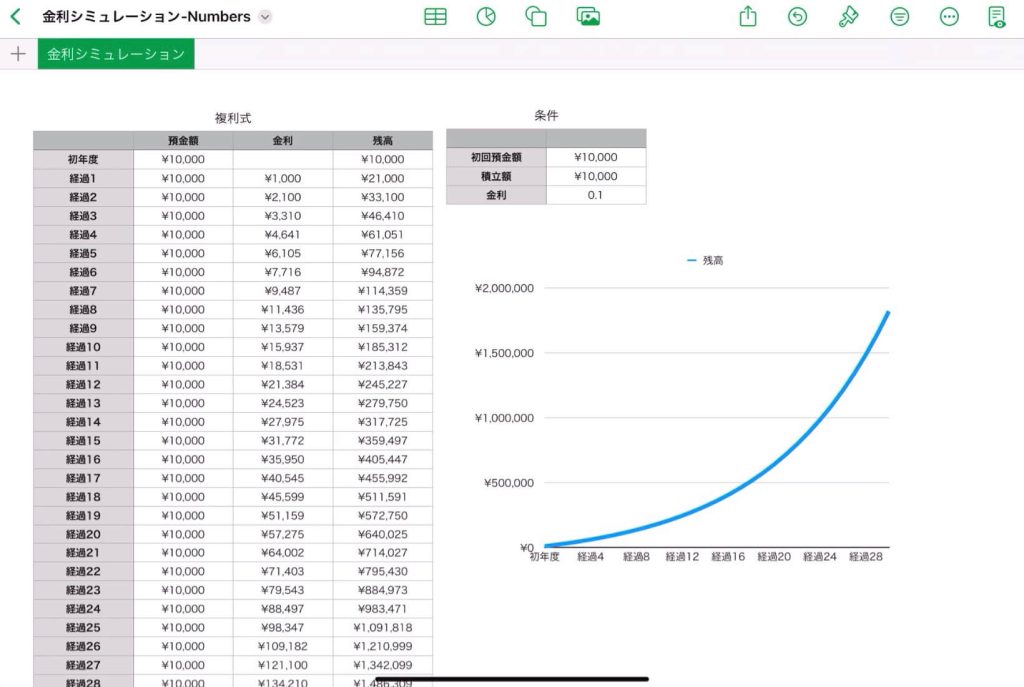
次のシミュレーションシートを作成します。

左表では30年後までの預金額、金利分の儲け、元利合計額(残高)を出力します。
右上の表では初回の投資額、積立額、金利を設定しています。
右下のグラフでは、口座残高の経過を表します。
1つ目の表のレイアウト
図のように必要事項を記入する
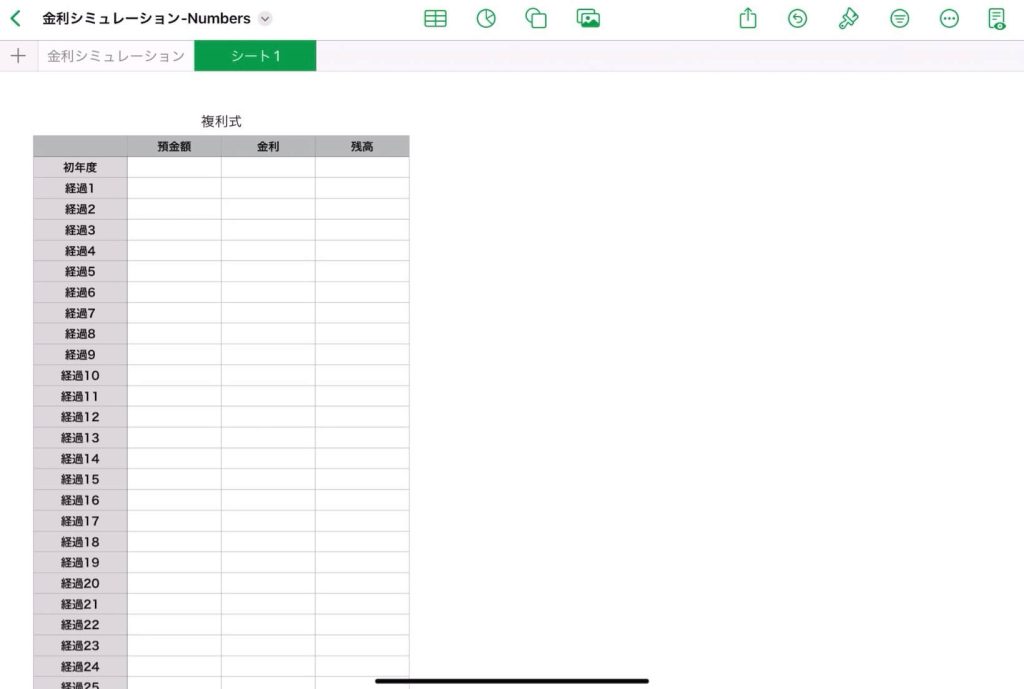
2つ目の表のレイアウト
①図のように必要事項を記入する
②左表のB2のセルに「=」を入力して, 「初回貯金額の値」をクリックする。
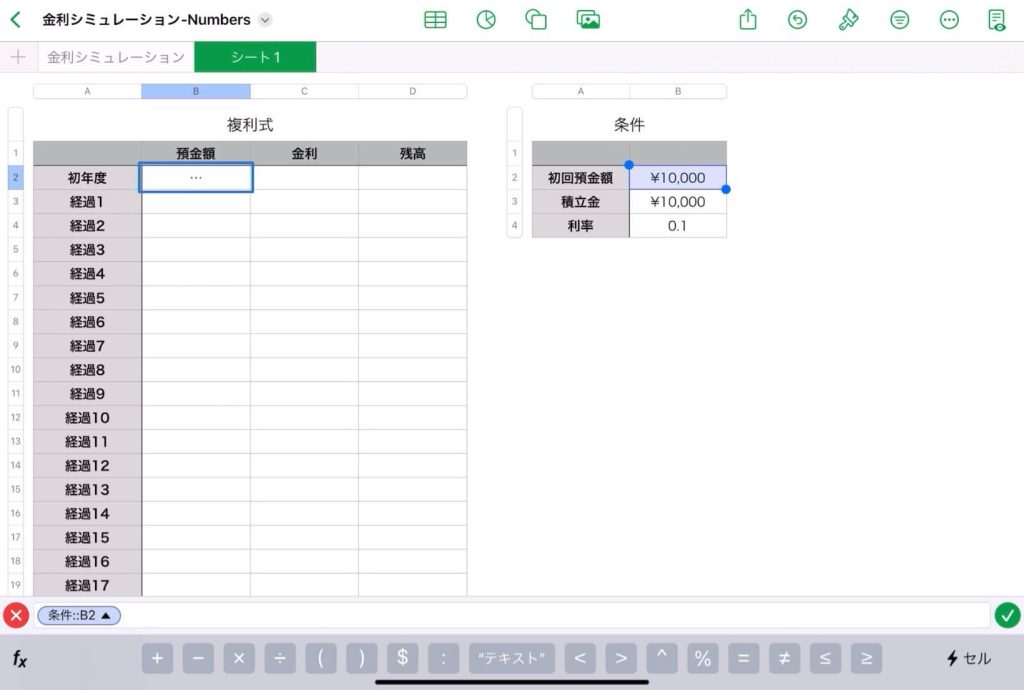
Numbersの機能
なお、Numbersでは図のように同じシートに表を2つ並べることができます。
下の図のようにやってください。
※ExcelやGoogleスプレッドシートではできません。

システムの作成①
左表のD2のセルに「=」を入力して, 「初年度の預金額の値」をクリックする。
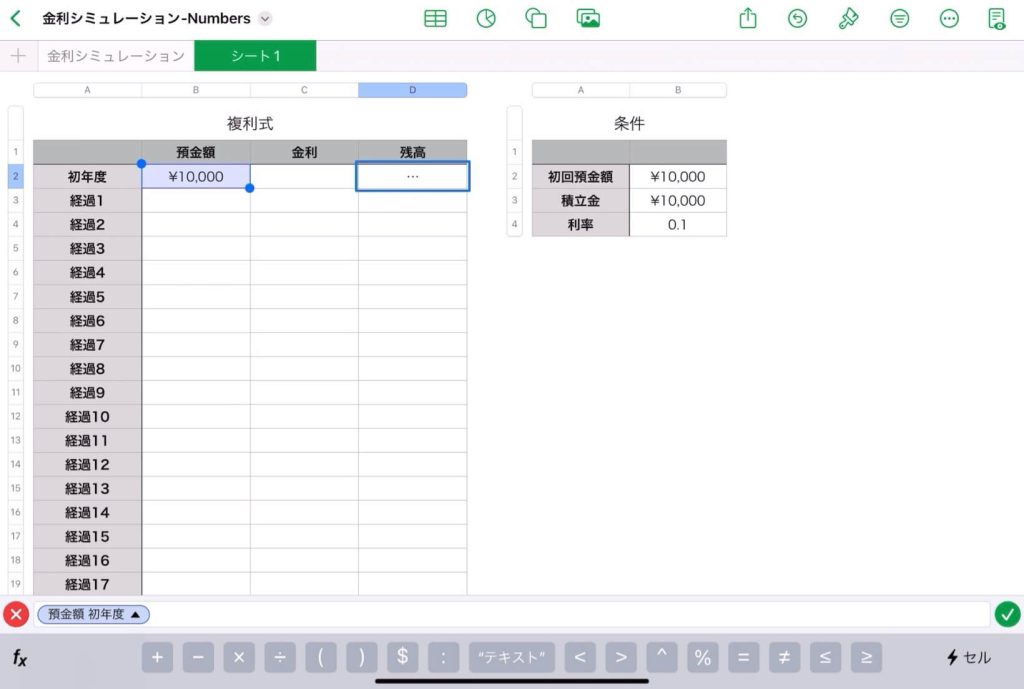
システムの作成②
左表のB3のセルに「=」を入力して, 「積立額の値」をクリックする。
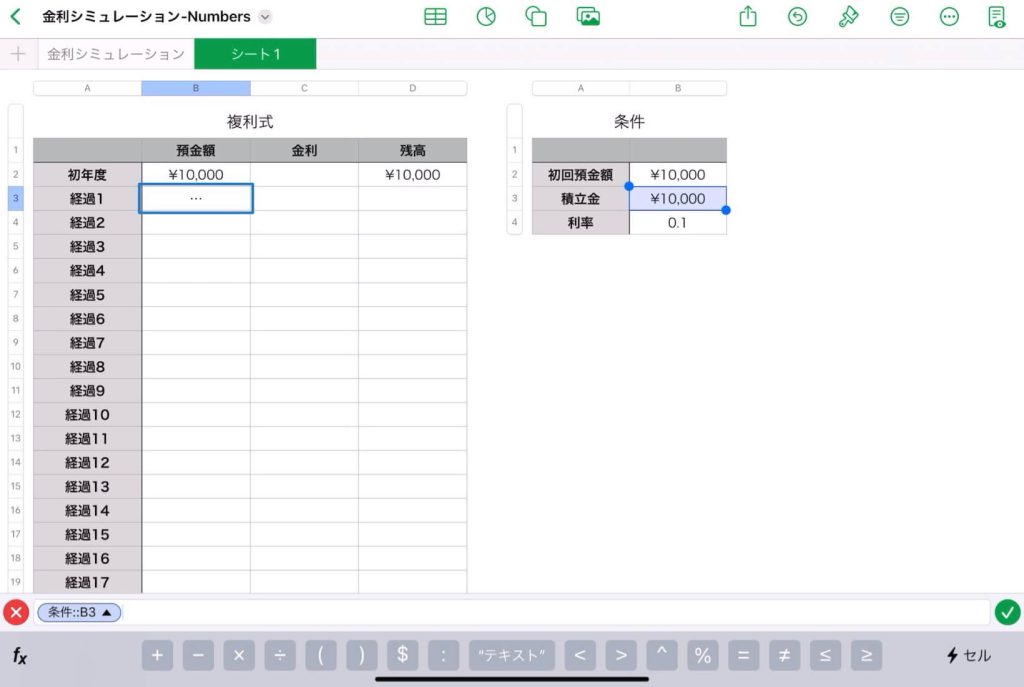
システムの作成③
左表のC3のセルに「=」を入力して, 「(初年度の残高の値)*(利率)」を入力する。
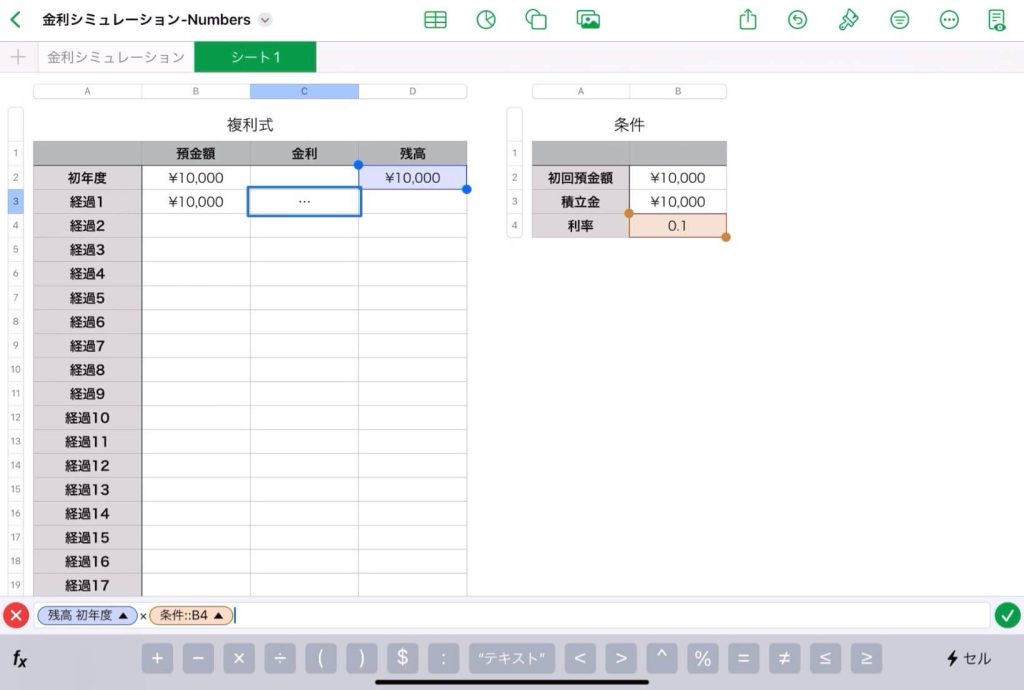
システムの作成④
左表のD3のセルに「=」を入力して, 「(初年度の残高)+(経過1の預金額)+(経過1の金利)」を入力する。
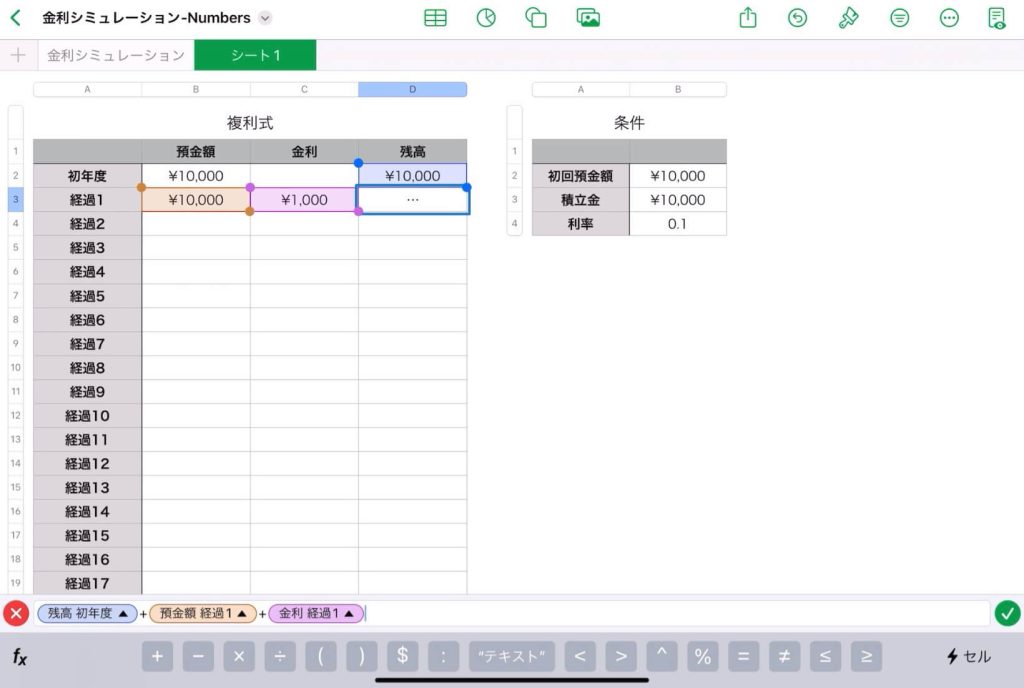
オートフィルの準備①
左表のB3のセルの参照を絶対参照にする。
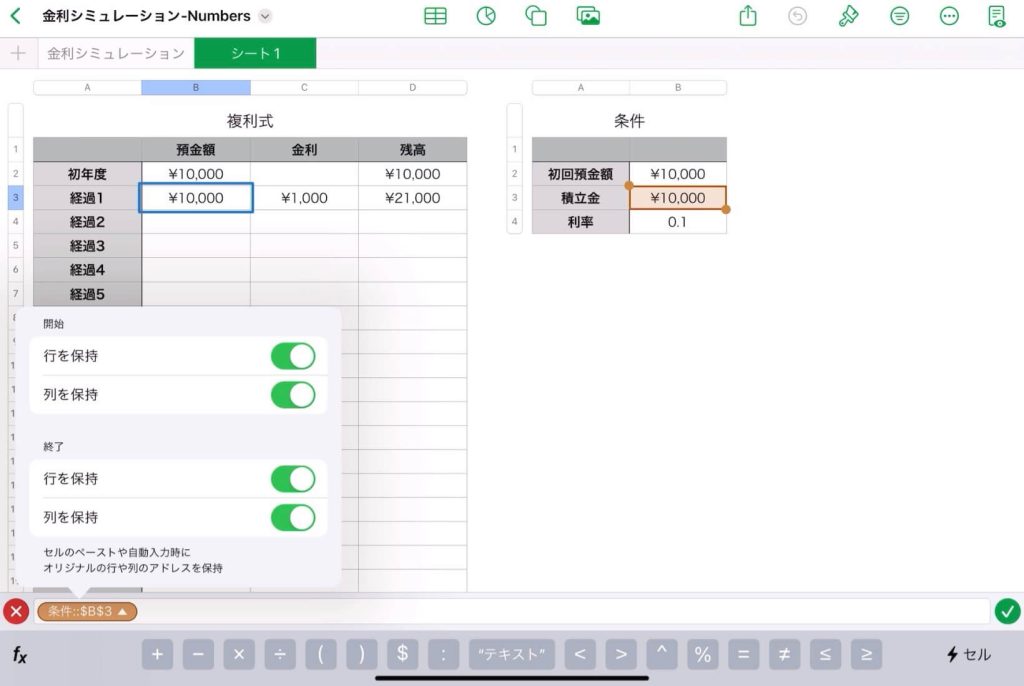
オートフィルの準備②
左表のC3のセルの、利率の参照のところだけを絶対参照にする。
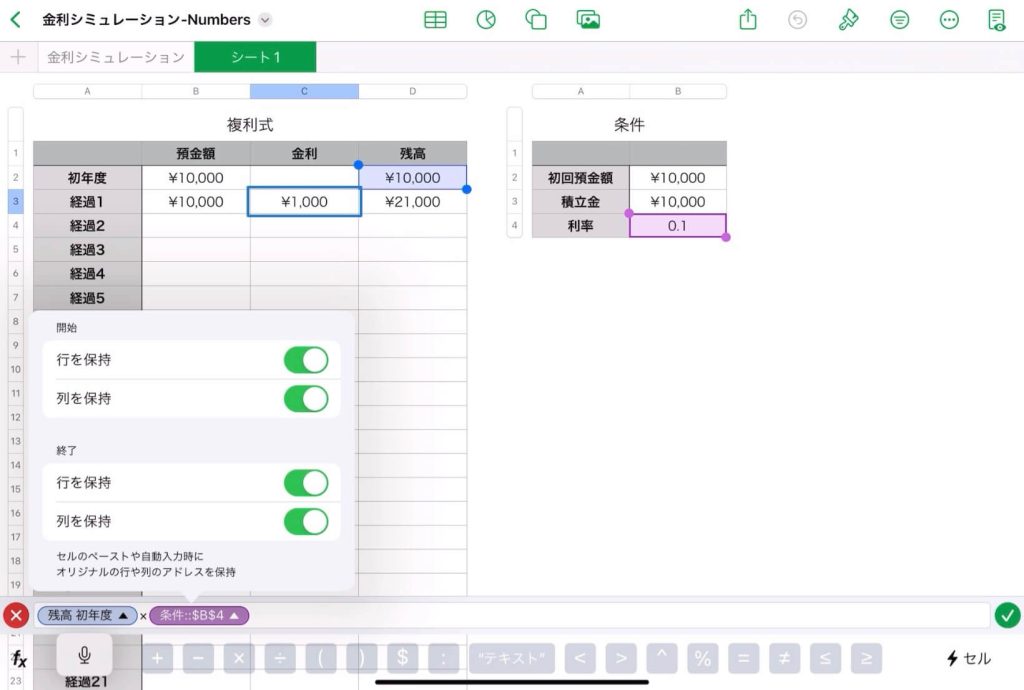
オートフィル
左表のB3とC3、D3のセルを全て選んで、オートフィルで表の下まで自動的に入力する。
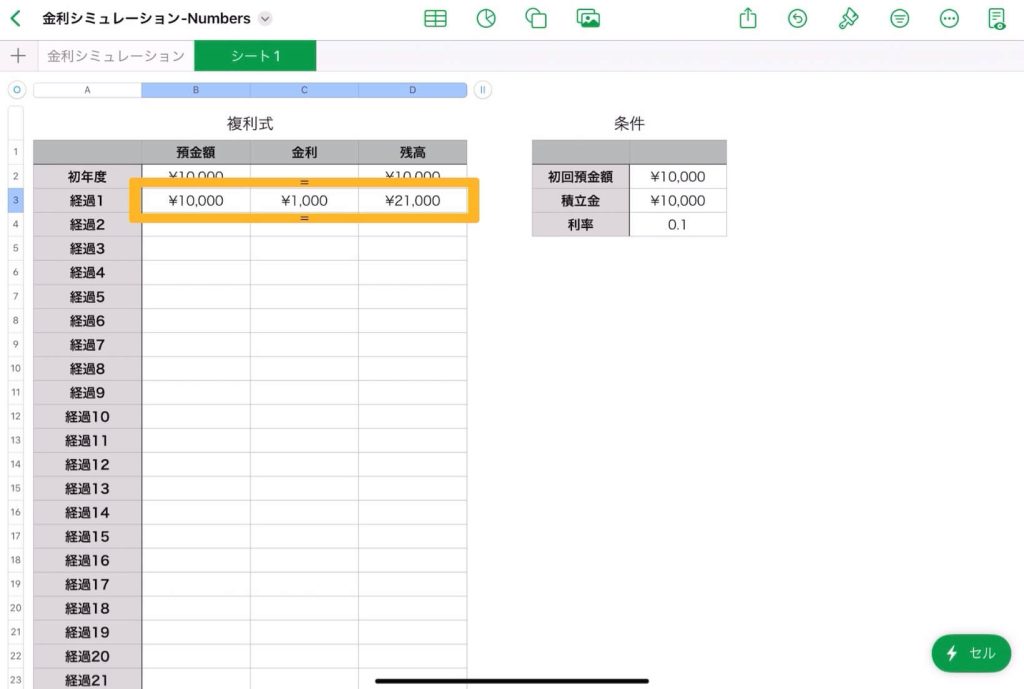
折れ線グラフの作成
①左表のA列とD列を選択する。
②上の「グラフ」のアイコンから、折れ線グラフを選択する。
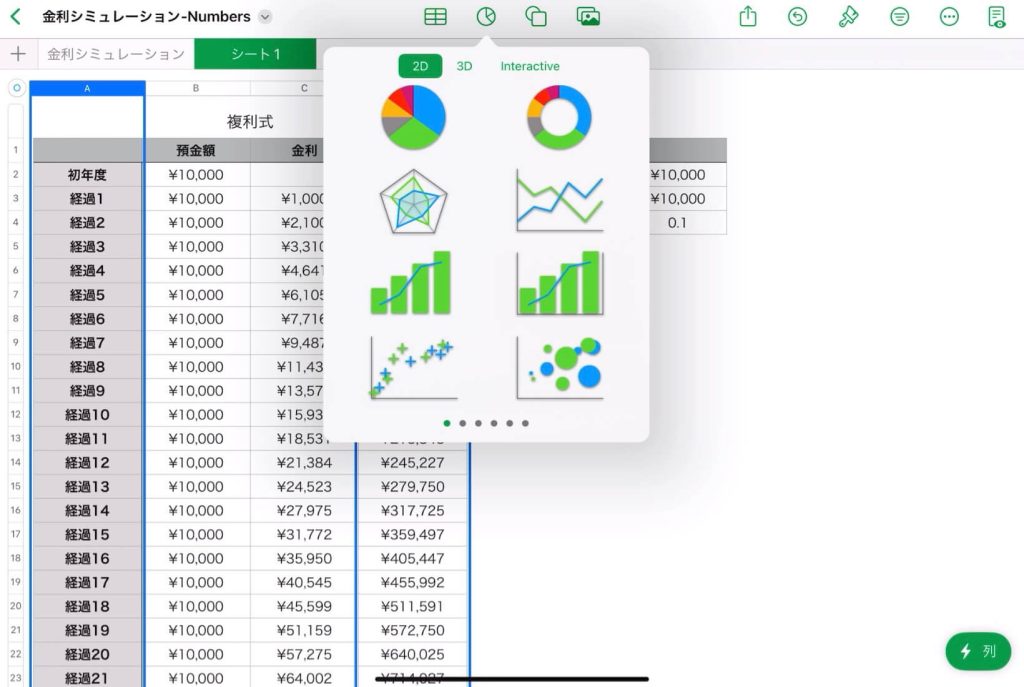
完成
2つ目の表の「初回貯金額」と「積立金」、「金利」を変えることで、いろいろな状況でシミュレーションできる。
このブログは、以上です。
金利のこと、複利を実用的に使いこなす術を紹介しました!
まとめノート
「複利法」とは
元金と利子(利息)の合計額を、次期の元金として計算する方法のこと。
定義式
元金 $a$ 円のみ預けた場合, 年利 $r$ の複利式による $n$ 年目の残高を $a_n$ とする. このとき,
$a_{n+1} = (1+r) a_n$
が成り立つ.
A. 預けっぱなし投資
初年度に $a$ 円を預けた場合は $a_n = a(1 + r)^n$ である.
定義式(積立)
毎年 $a$ 円ずつ積み立てる場合, 年利 $r$ の複利式による $n$ 年目の残高を $a_n$ とする. このとき,
$a_{n+1} = (1+r) a_n + a$
が成り立つ.
B. 積み立て投資
毎年 $a$ 円ずつ同額で積み立てた場合は次の通りである: $$a_n = \frac{a \{ (1 + r)^{n+1} - 1 \}}{r}$$
ポイント解説
単利法
元金のみに利子(利息)が付与される方法のこと。
例
各記号には次のような数値が入る;
各記号には次のような数値が入る;
| 記号 | 例 |
|---|---|
| 積立額 $a$ | 10万円 |
| 利率 $r$ | 0.01(1%) |
| $1 + r$ | 1.01 |
| $n$ 年後 | 30 |
また, $a_0 = a$ である。
B
$n$ 年目に積み立てた金額も含む。
B
$k$ 年目に預けた投資金は, $n$ 年目に $a(1+r)^{n-k}$ となる。これらの総和 $$\displaystyle \sum_{k=0}^n a(1+r)^{n-k}$$ を計算して公式を得る。



