- まとめ
- 表紙
- ①絵描き
- ②イメージ
- ③理解
ベジェ曲線とは
コンピュータで使われる滑らかな曲線のこと。
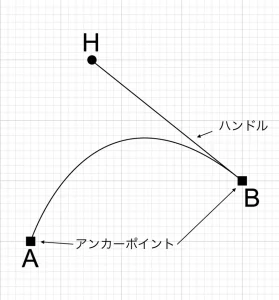
用語
アンカーポイントの $\mathbf{A}$ と $\mathbf{B}$ で曲線の始まりと終わりを指定する. $\mathbf{BH}$ のようなハンドルで曲線の曲がり具合を指定する. これらの点を総称して, 制御点という.
定義( $n$ 次ベジェ曲線 )
制御点 $\mathbf{P}_0$, $\mathbf{P}_1$, $\ldots$ , $\mathbf{P}_n$ をとる. $t \in [0, \ 1]$ のときの $\mathbf{P}(t)$ が描く軌跡をベジェ曲線という.
$$\displaystyle \mathbf{P}(t) = \sum_{k=0}^{n} {}_n \mathrm{C}_k (1-t)^{n-k} \ t^k \ \mathbf{P}_k$$
線分 $\mathbf{P}_0 \mathbf{P}_1$ と $\mathbf{P}_{n-1} \mathbf{P}_n$ は,
ベジェ曲線の始点と終点のそれぞれの接線である。
計算
曲線の両端点 $\mathbf{P}_0$, $\mathbf{P}_n$ がアンカーポイントになる. 他の点がハンドルになる.
ベジェ曲線を描くアルゴリズムが存在する.

イラスト

Illustratorでお絵描き

こんな図が簡単に描けるよ!
ベクター形式でデザインや設計のために利用されます。
ベジェ曲線の技法
2つのアンカーポイントで曲線の両端点を指定します。いくつかのハンドルを指定することで,曲線の曲がり具合を調整することができます。
直線の描き方
点を2つ打つだけで、線分が描けます。(アンカーポイントを指定。)
2次ベジェ曲線の描き方
点を2つ打ち、②の場所でハンドルを指定しました。これだけで様々な曲線が描けます。この曲線を2次のベジェ曲線といいます。
3次ベジェ曲線の描き方
点を2つ打ち、はじめの①と、あとの②の場所で両方ともハンドルを指定しました。
かなり複雑な曲線も描けます。この曲線を3次のベジェ曲線といいます。
ベジェ曲線のイメージ
今日の授業
ベジェ曲線が描かれる仕組み(アルゴリズム)を紹介します。
ド・カステリョのアルゴリズム
①制御点の順番を決める
次のベジェ曲線を考えます。アンカーポイントは $\mathbf{P}_0$ と $\mathbf{P}_3$ が該当します。

制御点の順番を $\mathbf{P}_0$→$\mathbf{P}_1$→$\mathbf{P}_{2}$→$\mathbf{P}_3$ とします。
②同じ比に内分する点の作図
隣り合う制御点を $m:n$ に内分する点を作図します。

今回は、3つの点ができます。
③同じ比に内分する点の作図
いまできた3点について,さらに隣り合う点同士を,また $m:n$ に内分する点を作図します。

今回は、2つの点ができます。
④同じ比に内分する点の作図
いまできた2点について,さらに隣り合う点同士を,また $m:n$ に内分する点を作図します。

この作業を繰り返した結果、1点だけになりました。
この最後の点がベジェ曲線上の点と一致します。
⑤他の点も作図
他の比でも同じ作業をしていって、たくさん点を作ったら、その集まりがベジェ曲線になります。
$m:n = 1:0$ のとき、はじめのアンカーポイントの $\mathrm{P}_0$ です。
$m:n = 0:1$ のとき、ゴールのアンカーポイントの $\mathrm{P}_1$ です。
ベジェ曲線の数式の理解
ベジェ曲線の定義について
ベジェ曲線
定義
平面内の点 $\mathbf{P}_0$, $\mathbf{P}_1$, $\ldots$ , $\mathbf{P}_n$ と $0 \leqq t \leqq 1$ について,次の式で表される曲線を $n$次ベジェ曲線という。
$$\displaystyle \mathbf{P}(t) = \sum_{k=0}^{n} {}_n \mathrm{C}_k (1-t)^{n-k}t^k \mathbf{P}_k$$
3次ベジェ曲線で説明をします。4点 $\mathbf{P}_0$, $\mathbf{P}_1$, $\mathbf{P}_2$, $\mathbf{P}_3$ が制御点に該当します。
ドカステリョのアルゴリズムを数式で表して、ベジェ曲線の方程式を求めます。
①図と式を対応させる
$\mathbf{P}_0$ と $\mathbf{P}_3$ がベジェ曲線の端点(アンカーポイント)になるべき点です。

イラストレータでは、線分 $\mathbf{P}_0 \mathbf{P}_1$ と $\mathbf{P}_3 \mathbf{P}_2$ がハンドルと対応する。
②制御点を結ぶ線分の内分点をつくる
$\mathbf{P}_0$→$\mathbf{P}_1$ と $\mathbf{P}_1$→$\mathbf{P}_2$, $\mathbf{P}_2$→$\mathbf{P}_3$ の間をそれぞれ $m: n = t : 1-t$ に内分する点を $\mathbf{P}_{1,0}(t)$, $\mathbf{P}_{1,1}(t)$,$\mathbf{P}_{1,2}(t)$ とします:
- $\mathbf{P}_{1,0}(t) = (1-t) \mathbf{P}_0 + t\mathbf{P}_1$
- $\mathbf{P}_{1,1}(t) = (1-t) \mathbf{P}_1 + t\mathbf{P}_2$
- $\mathbf{P}_{1,2} (t)= (1-t) \mathbf{P}_{2} + t\mathbf{P}_3$

③更に内分点をつくる
いまできた点について,$\mathbf{P}_{1,0}$→$\mathbf{P}_{1,1}$ と $\mathbf{P}_{1,1}$→$\mathbf{P}_{1,2}$ の間をそれぞれ,また $m: n = t : 1-t$ に内分する点を $\mathbf{P}_{2,0}(t), \mathbf{P}_{2,1}(t)$ とします:
- $\mathbf{P}_{2,0}(t) = (1-t) \mathbf{P}_{1,0} + t\mathbf{P}_{1,1}$
- $\mathbf{P}_{2,1}(t) = (1-t) \mathbf{P}_{1,1} + t\mathbf{P}_{1,2}$

④もういちど繰り返す
さらに,点$\mathbf{P}_{2,0}(t)$ → $\mathbf{P}_{2,1}(t)$ の間を結んで,また,$m: n = t : 1-t$ に内分する点 $\mathbf{P}(t)$ を決める:
- $\mathbf{P}(t) = (1-t) \mathbf{P}_{2,0} + t\mathbf{P}_{2,1}$

⑤式を整理する
点 $\mathbf{P}_{2,0}(t)$ と $\mathbf{P}_{2,1}(t)$ は,今までの式を組み合わせると,初めの制御点 $\mathbf{P}_0$, $\mathbf{P}_1$, $\mathbf{P}_2$, $\mathbf{P}_3$ で表すことができる。$\mathbf{P}(t)$ をはじめの制御点で表すと,
$\mathbf{P}(t) = (1-t) \mathbf{P}_{2,0} + t\mathbf{P}_{2,1}$
$= (1-t)^3 \mathbf{P}_0$ $+3(1-t)^2 t \mathbf{P}_1$ $+3(1-t) t^2 \mathbf{P}_2$ $+ t^3 \mathbf{P}_3$
$\displaystyle = \sum_{k=0}^{3} {}_3 \mathrm{C}_k \ (1-t)^{3-k} \ t^k \ \mathbf{P}_k$
となる。
実数 $t(0 \leqq 0 \leqq 1)$ を1つ決めて,内分比 $m:n=t:(1-t)$となるように作った点が $\mathrm{P}(t)$ であった。
$t$ を0から1に動かしたときの軌跡である方程式 $\mathrm{P}(t)$ が3次ベジェ曲線である。
⑥一般化する
一般の $n$ 次ベジェ曲線の数式は次のとおりである:
$$\displaystyle \mathbf{P}(t) = \sum_{k=0}^{n} {}_n \mathrm{C}_k (1-t)^{n-k}t^k \mathbf{P}_k$$

イメージにピッタリだね!

