複利法について

複利法が使われている場面、複利法の数学、Excelでのシミュレーションを学びます！

【世の中】利子／金利・複利式とは
複利法の使いどころ
【理解】複利式の数学的な解説
【表計算】Excelで複利式をシミュレーション
- 30年後の預金額のシミュレーション
複利シミュレーション（積立額の自動算出）
複利シミュレーション（推移グラフ）
まとめノート

【世の中】利子／金利・複利式とは

現代の金利事情

いまの金利が低すぎるので、銀行預金の金利を調べてみました。（2023年11月30日）

複利法の使いどころ

複利法の使いどころ

現代の金利事情（2023.11.30）

貯金、投資、保険、ローン、借金…

いま現在の銀行の「金利」は、どれくらいなのか調べてみました。
金利は「年利〇〇%」で表記することが通例のようです！

主要銀行の金利比較

すべて「通常貯金（普通預金）」に対する金利です。
※他の貯金の仕方だと"少し"金利が高い場合があります！

ゆうちょ銀行→「0.001%」（金利一覧-ゆうちょ銀行）
みずほ銀行→「0.001%」（預金金利・利率｜みずほ銀行）
UFJ銀行→「0.0010%」（円預金金利｜三菱UFJ銀行）
三井住友銀行→「0.001%」（円預金金利：三井住友銀行）
りそな銀行→「0.001%」（円預金金利|口座を開きたい｜りそな銀行）

※すべて2023年11月30日現在の情報*

Wow!!ぜんぶ金利低すぎるorz
不景気ですね。

もう少し銀行の金利比較

バブルの頃は、定期預金が年利5%を越えていたようです。（今の時代では信じられないですね！）

PayPay銀行→残高100万円未満「0.001%」, 残高100万円以上「0.001%」（円預金金利・預金金利-PayPay銀行）
楽天銀行→「0.02%」（定期預金や外貨預金の預金金利｜楽天銀行）

※すべて2023年11月30日現在の情報*

通常貯金ではなく、「定期預金」をザッと見ると、「0.002%」の金利でした。

積立貯金をするときの複利

まず，複利の計算に必要な情報を整理する。

毎年同じ金額を積み立てて預金したとき、○○年後には預金額（元利合計額）はいくらになっているか？

次の表の情報から、未来の元利合計額が算出する。

意味	例（預金）	例（借金）	文字
発生額（&積立額）	10万円	50万円	$a$
利率	0.01（1%）	0.1（10%）	$r$
$1 + r$	1.01	1.1	$b$
何年後か？	30年後	30年後	$n$

◎公式の変数の意味と事例の表◎

金利の付け方の整理

単利法

単利法は自分が預けたお金（預金額-元金）にしか「利子」が付きません。

国債などの金利は、単利だそうです。

複利法

複利法は、自分が預けたお金と、得た利子に対しても、さらに「利子」がつきます。

銀行の預金などの金利は、複利だそうです。

単利と複利の違い

単利と複利の言葉だけ聞いていても、単利と複利の違いがあまり判りません。

■単利の計算例

〜例えば（金利10%で100万円預けた場合）〜
100万円預けた場合
→1年後の利子（1,000,000×0.1）→利子「10万円」です。
→2年後の利子→変わらず利子「10万円」です。

■複利の計算例

〜例えば（金利10%で100万円預けた場合）〜
→1年後の利子（1,000,000×0.1）→利子「10万円」です。
→2年後の利子（1,100,000×0.1）→変わらず利子「11万円」です。

※単利も複利も説明を容易にするために、利子を高めの10%にしました。
計算するときは「10%=0.1」にしてくださいね！

ちなみに「0.001%」というのは、計算の際は「0.00001」にします。
かなり低い数値ですね。

いま「10%」という幻の金利で計算しました。
「1年で1万円」の差がでました。
しかし、単利と複利は、長期的に見た方が、その違いが非常に顕著に見えます。

アインシュタインの名言（複利の不思議）

Compound interest is the 8th wonder of the world.
He who understands it, earns it… he who doesn't…pays it.
Albert Einstein

JackとJillの物語（年利10%）

【弟のジャック】姉のジルと遊んでいる最中に頭をケガしてしまい、大学に進学できませんでした。18歳から働き始めて、毎月4万円ずつ8年間だけ積立投資をしました。その後はお金を積み立てせずに、投資金額の累計は384万円（毎月4万円 × 12カ月 × 8年）のまま65歳まで運用を続けました。

【姉のジル】弟のジャックと遊んでいたときの罪の意識もあり、医大に進学しました。26歳で働き始めて、毎月4万円ずつ65歳までの40年間積立投資をしました。結果、ジルの投資金額の累計は1,920万円（毎月4万円 × 12カ月 × 40年）です。
【引用】
①リック・イーデルマン, 家庭の金銭学, きんざい
②リベラルアーツ大学, 【薬が毒に？】複利のすごさが分かるエピソードと複利が壊す「生きるセンス」3つを解説, 2024.10.24アクセス

$72$ の法則

複利で資産を２倍にするために必要な期間の簡単な計算式のこと

$72 \div (\textrm{利率}[\%])$ $=\textrm{(2倍にするために必要な複利の回数)}$

［例］年利率 $3 \%$ ならば, $72 \div 3 = 24$ 年かかる。

【理解】複利式の数学的な解説

初期投資額 $a$ 円とする。複利式での利子率を $r$ とします。複利式で $n$ 回の利子を受け取った後の元利合計を $a_n$ 円とします。

初期投資のみ（預けっぱなし）の場合

$a_n = a(1+r)^n$

複利式での資金の変化を考えてみよう。例えば, 利率が $10\%$ で $10$ (万)円を投資した場合, $n$ 年後には $10 \times (1.1)^n$ 万円になります。

基本の解法

利子率 $r$, 投資額 $a$とする。複利式で $n$ 回の利子を受け取った後の元利合計 $a_n$ は次の通り: $$a_n = a (1+r)^n$$

$n$ 回で受け取った利子の合計は $a(1+r)^n - a$ である。

複利式は、ある年度に受け取った利子にも、その次年度に利子が付くという方式である。

年利で考えると(次年度の利子)=(今年度までの元利合計)×(利率)である。

これより(次年度の元利合計)=(今年度までの元利合計)×(１＋利率)が成り立つ。

例題. 複利の利子率が $10\%$, 初回の投資額を $10$ (万)円とする。$10$ 回目の利子を受け取った後の元利合計および利子はいくらか。

与えられた条件から $n$ 回目の利子を得た後の元利合計を $a_n$ とすると $a_n = 10 \times (1.1)^n$ (万) である。

$r = 0.1$, $a = 10$(万).

$n=10$ のとき $a_{10} = 10 \times (1.1)^{10}\fallingdotseq 25.9374$ である。

ゆえに, 10回目の利子を受け取った後の元利合計は 259,374円である。

投資金額は 10万円であるので、受け取った利子は $25.9374-10$ $=15.9374$ (万) である。

ゆえに10回で受け取った利子の総額は 159,374円である。

単利式の場合, 10回で受け取る利子の総額は 10万円である。

複利の利子率が $10\%$, 投資額を $10$ (万)円とします。単位は(万)として年利で考えます。

1年後の利子は $10 \times 0.1$ です。

1年後の元金と利子の合計は: $10 \times (1+0.1)$ $= 10 \times 1.1$.

2年後の利子は $(10 \times 1.1) \times 0.1$ です。

2年後の元金と利子の合計は: $(10 \times 1.1) \times (1 + 0.1)$ $= 10 \times (1.1)^2$.

3年後の利子は $(10 \times (1.1)^2) \times 0.1$ です。

3年後の元金と利子の合計は: $(10 \times (1.1)^2) \times (1+0.1)$ $= 10 \times (1.1)^3$.

この規則で $n$ 年後の元利合計が分かりますね！

毎回同額積立（ $a$ 円ずつ）の場合

$\displaystyle a_n=\frac{a}{r}\{ (1+r)^{n+1} -1 \}$

複利式で、毎回同額ずつを積み立てた場合の資金の変化を考えてみよう。

例えば, 年利率が $0.1(10\%)$ で $10$ (万)円を毎年積み立てた場合, $n$ 年後には $$\frac{10 \{ (1.1)^{n+1} -1\}}{0.1} \text{(万)円}$$になります。

基本の解法

利子率 $r$, 毎回の積立額 $a$ とする。複利式で $n$ 回の利子を受け取った後の元利合計は次の通り:

$\displaystyle \sum_{k=0}^n a (1+r)^k$ $\displaystyle = \frac{a}{r} \{(1+r)^{n+1} - 1 \}$

ただし, $n$ 回目の利子を受け取った回に積み立てた額も含む。

証明.

$0 \leqq k \leqq n$ とする。初回から数えて$n$ 回目の利子を受け取るとき時点では, $k$ 回目に積み立てた額 $a$ には利子を $n-k$ 回付くため元利合計は $a(1+r)^{n-k}$ となる。

$k=0$ のときは初回に投資した $a$ を指す。初回から数えて $n$ 回目の利子を受け取る時点では, 利子が $n$ 回すべて付くため, 元利合計は $a(1+r)^{n-0} =a(1+r)^n$ となる。

$k=n$ のときは $n$ 回目の利子を受け取った時点での積立額を指す。これに利子は未だ付かないので, 元利合計は元金のままで $a(1+r)^{n-n} =a$ となる。

$n$ 回目の利子を受け取る時点での元利合計の総額は, 各回の積立額に利子が付いた額の和である。したがって, $$\sum_{k=0}^n a (1+r)^{n-k}$$ が求めるものである。

$\displaystyle \sum_{k=0}^n a (1+r)^{n-k}$ $= a(1+r)^n + \cdots + a(1+r) +a$.

$\{ a (1+r)^{n-k} \}_{0 \leqq k \leqq n}$ は等比数列である。また, $\{ a (1+r)^{k} \}_{0 \leqq k \leqq n}$ は項を足す順番を逆にした数列で初項 $a$, 公比 $1+r$ の等比数列である。等比数列の和の公式より

$\begin{aligned}
&\sum_{k=0}^n a (1+r)^{n-k} \\
&= \sum_{k=0}^n a (1+r)^{k} \\
&= \frac{a \{ (1+r)^{n+1} - 1 \}}{(1+r) - 1} \\
&= \frac{a}{r} \{ (1+r)^{n+1} - 1 \}.
\end{aligned}$

初項 $a$, 公比 $R$ の等比数列の和の公式は次の通り: $$\sum_{k=0}^n a R^{k} = \frac{a(R^{n+1} -1)}{R-1}$$

ゆえに, $n$ 回目の利子を受け取った後の積立の元利合計の総額は $$\frac{a}{r} \{ (1+r)^{n+1} - 1 \}$$ である。

複利の年利率が $0.1$ $(10\%)$, 投資額を $10$ (万)円とします。

各年度で投資した $10$ 万円の10年間の推移を表にしました。

積立年度	投資額	利子を含めた10年後の金額
初年度	10万円	$10(1.1)^{10}$ 万円
1年後	10万円	$10(1.1)^{9}$ 万円
2年後	10万円	$10(1.1)^{8}$ 万円
$\vdots$	$\vdots$	$\vdots$
9年後	10万円	$10 \times (1.1)$ 万円
10年後	10万円	$10$ 万円
合計額	110万円	$185.311$ 万円

10年後の元利合計の総額は

$10(1.1)^{10}$ $+10(1.1)^{9}$ $+10(1.1)^{8}$ $+ \cdots$ $+10 \cdot (1.1)$ $+10$

です！

毎回同額積立（ $a$ 円ずつ）の場合

$a_{n+1} = (1+r)a_n + a$

→ $\displaystyle a_n=\left(a_1 + \frac{a}{r} \right) (1+r)^n - \frac{a}{r}$

複利で毎回同額の積立をする場合の漸化式 $a_{n+1} = (1+r)a_{n} + a$ と一般項を扱ってみよう。

複利式の漸化式

利子率 $r$, 毎回の積立額 $a$ とする. $a_n$ を $n$ 回目の利子を受け取った後の元利合計とする. $$a_{n+1} = (1+r)a_n + a.$$

複利式積立の公式

利子率 $r$, 毎回の積立額 $a$ とする. 初回の投資額を $a_1$ とする. $n$ 回目の利子を受け取った後の元利合計: $$\left(a_1 + \frac{a}{r} \right)(1+r)^n - \frac{a}{r}$$

ただし, $n$ 回目の利子を受け取った回に積み立てた額も含む。

※ 利子率が $r$ で, $n$ 回目の利子を受け取りその回の積立額 $a$ も含めた元利総額を $a_n$ としています。

複利式で年利積立の場合の条件式は(次年度の残高)=(今年度の残高)×(１＋利率) + (積立金)である。

初回の元金を $a_0$ とする。$n$ 年目の残高を $a_n$ とすると $a_{n+1}$ $= (1+r)a_n + a$ となる。

［基本の解法］積立額（複利式）の漸化式 $a_{n+1} = (1+r)a_{n} + a$ から一般項を導く解法は $a_{n+1} = pa_n +q (p \neq 1)$ の形の漸化式から一般項を導く方法を利用する。

例題. 複利の利子率が $10\%$, 毎回の積立額が $10$ (万)円, 初回の投資額を $50$ (万)円とする。$n$ 回目の利子を受け取った後の資産はいくらか。

与えられた条件から $n$ 年目の資産 $a_n$ が満たす漸化式は $a_{n+1} = 1.1 a_n + 10$, $a_0 = 50$ とできる。

$r = 0.1$, $a = 10$(万), $a_1 = 50$(万).

この漸化式は $a_{n+1} +100 = 1.1(a_n + 100)$ と変形できる。

$a_{n+1} = pa_n +q$ は $x = px+q$ を満たす $x$ を用いて, $a_{n+1} - x = p(a_n -x)$ と変形できる。

$\displaystyle x = -\frac{a}{r}$ は積立額を利率で割った値のマイナスを付けたもの.

$\{ a_n + 100 \}_n$ という数列は公比 $1.1$ の等比数列である。また, 初項は $a_0+100 = 50+100 = 150$ である。ゆえに, $a_n + 100 = 150 (1.1)^n$ とできる。

$b_n = a_n+100$ と置くと, $b_{n+1} = a_{n+1} + 100$ である。$a_{n+1} +100 = 1.1(a_n +100)$ は $b_{n+1} = 1.1 \cdot b_n$ となる。

以上から $$a_n = 150 (1.1)^n-100$$ を得る。

複利の利子率が $10\%$ $(r=0.1)$, 毎回の積立額が $10$ (万)円, 初回の投資額を $50$ (万)円とする。

$n$ 回目の利子を受け取った後の資産の定義式は

$a_{n+1}$ $= (1+0.1)a_n + 10$

となる。この数列の一般項を導くと

$a_n$ $= 150 (1.1)^{n}-100$

になる:

動画による解説

積立の場合（解説動画）

10秒チェックテスト

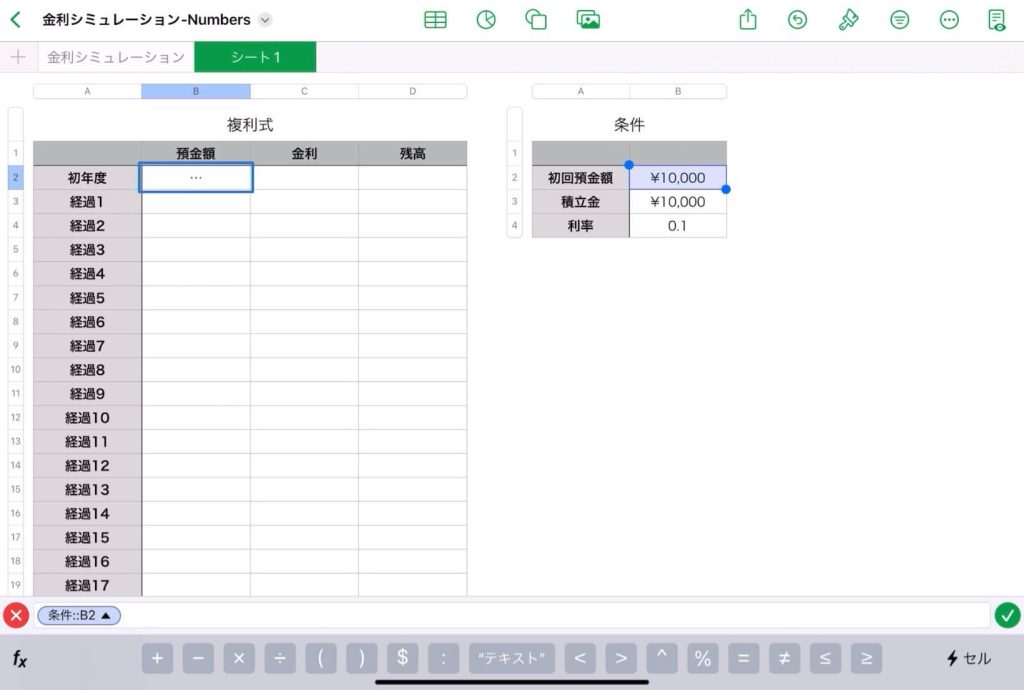
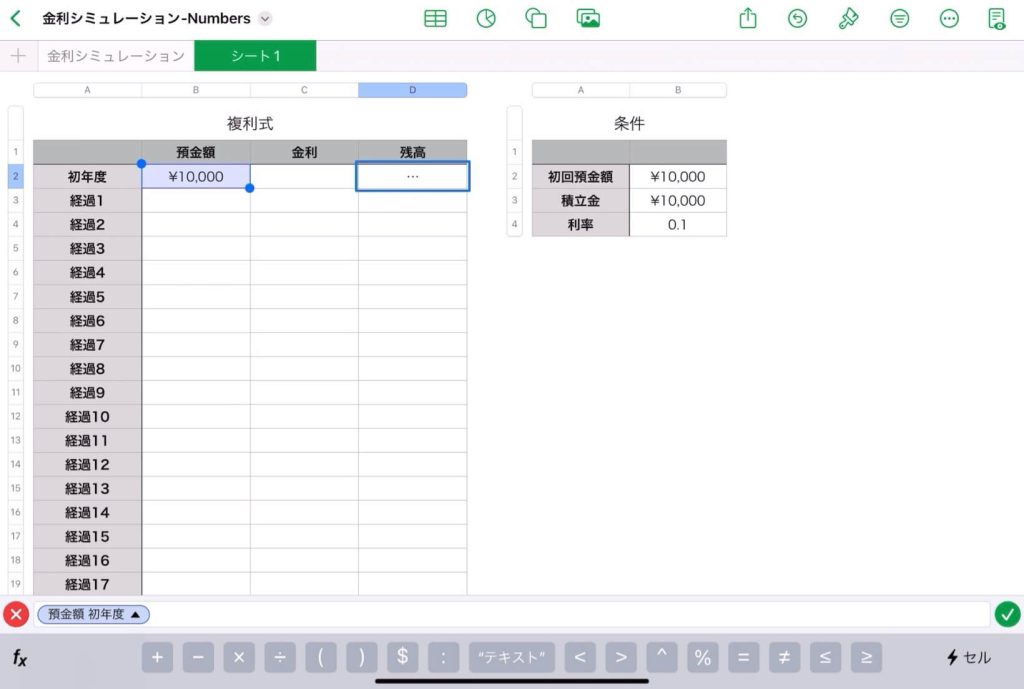
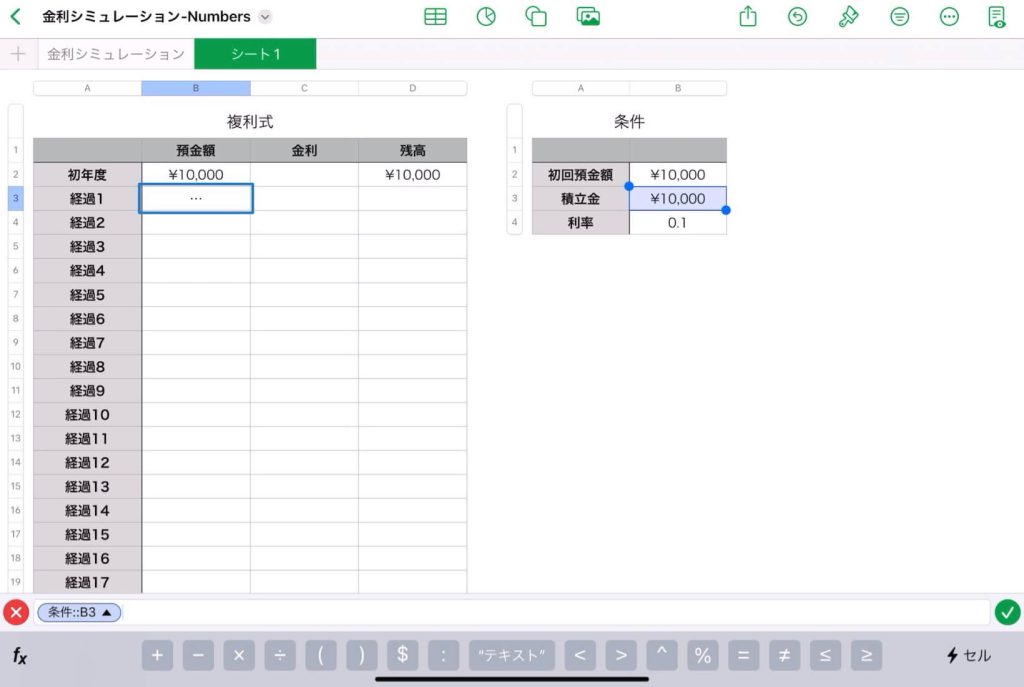
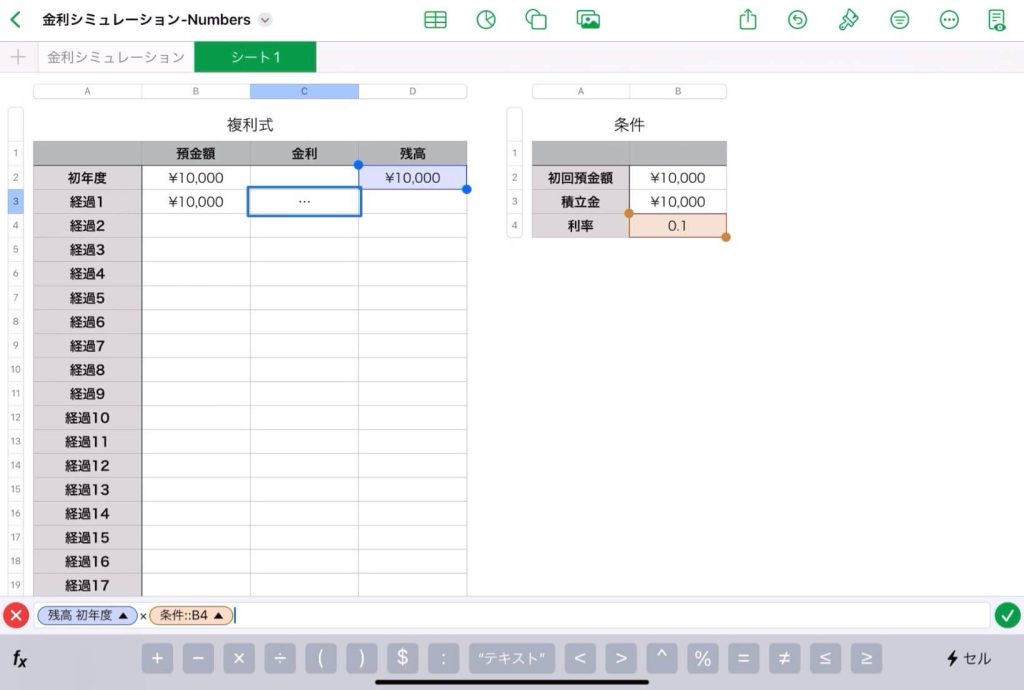
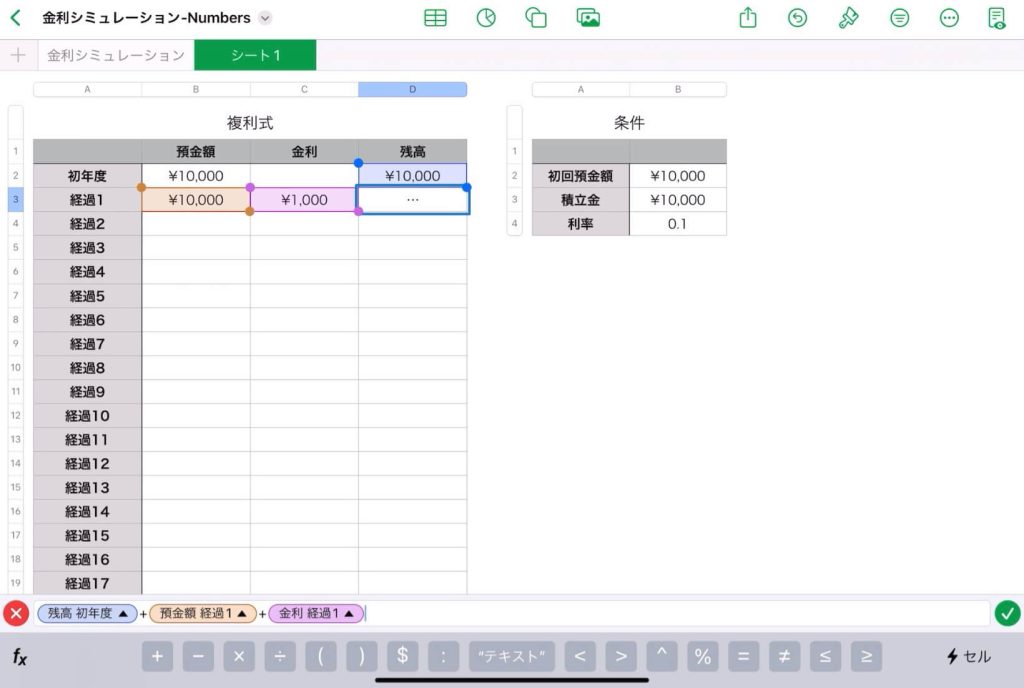
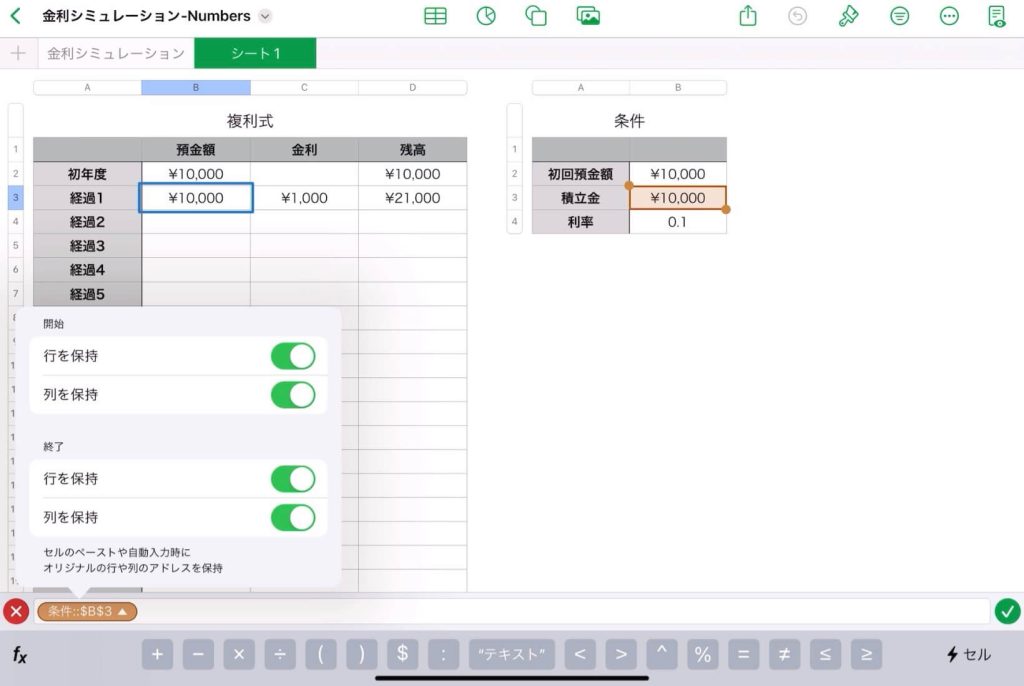
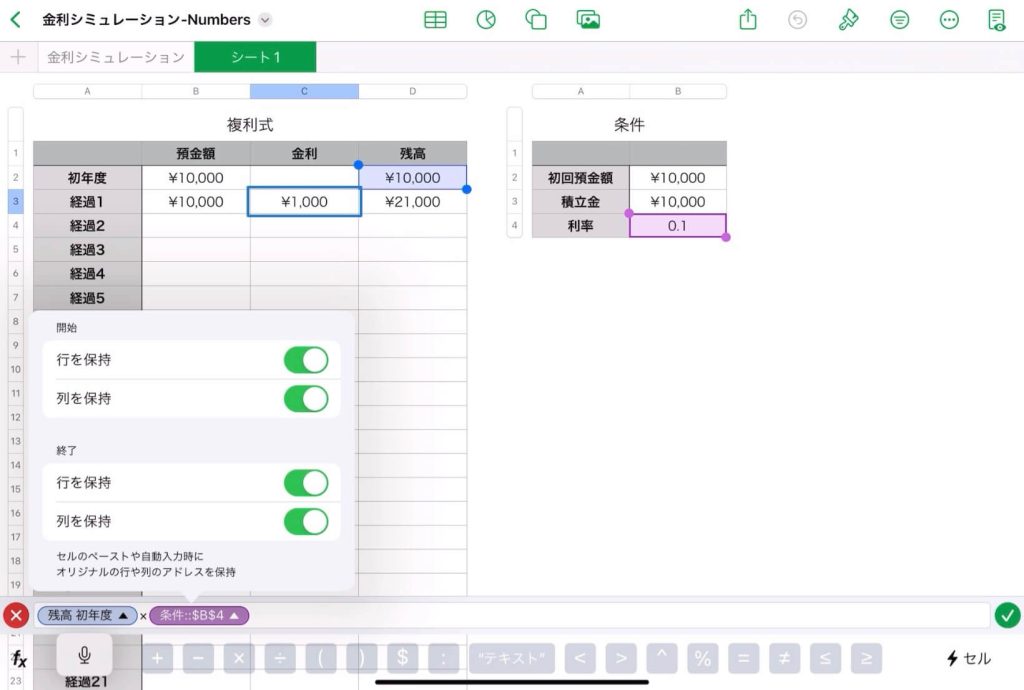
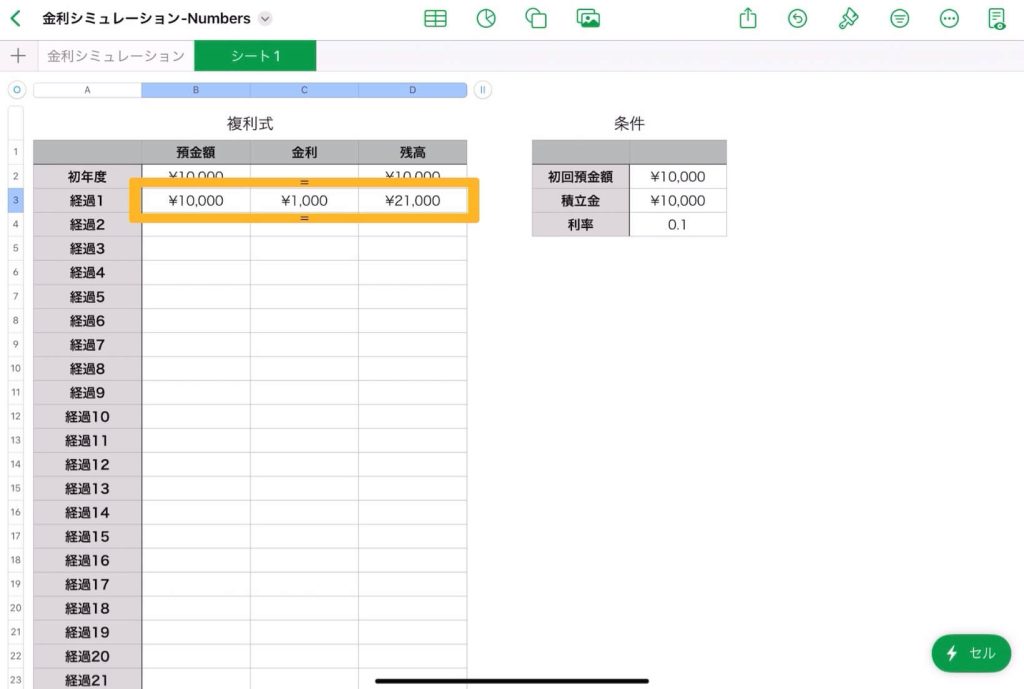
【表計算】Excelで複利式をシミュレーション

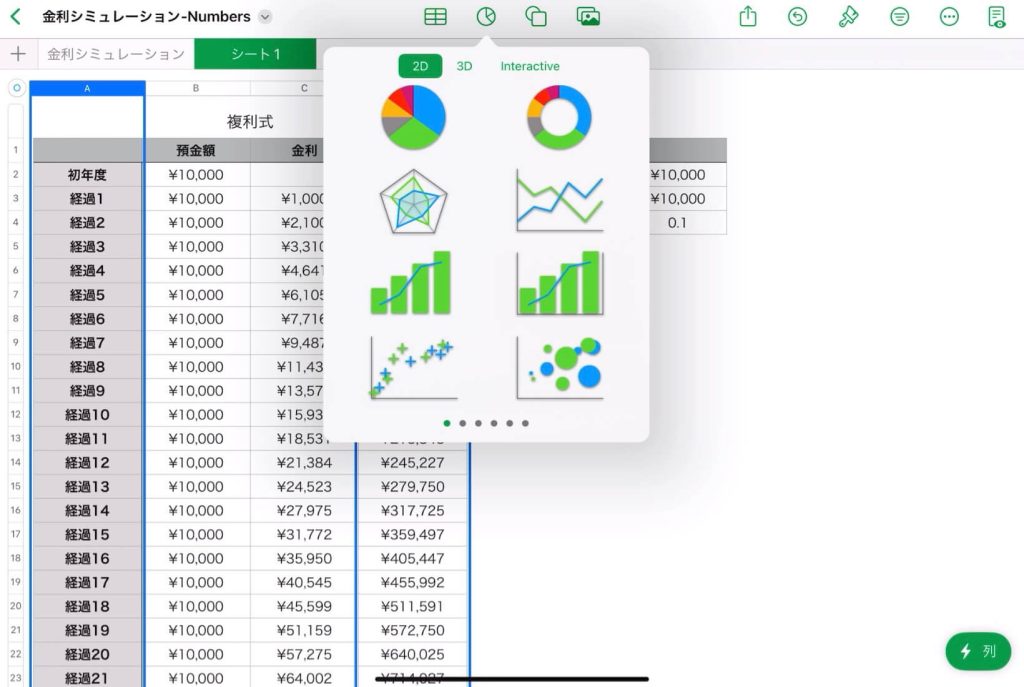
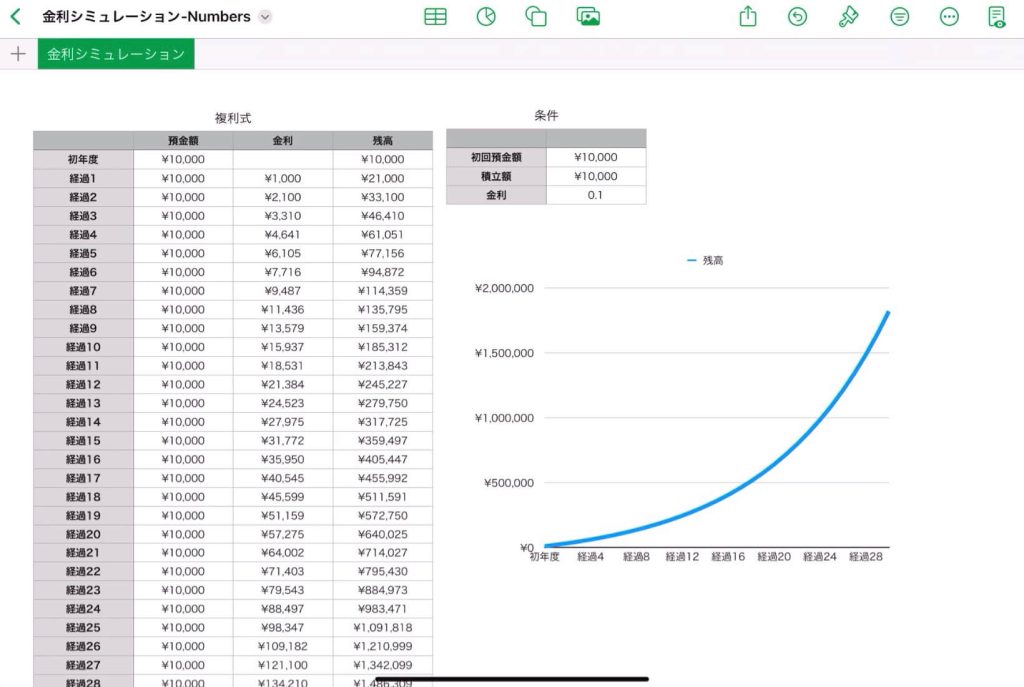
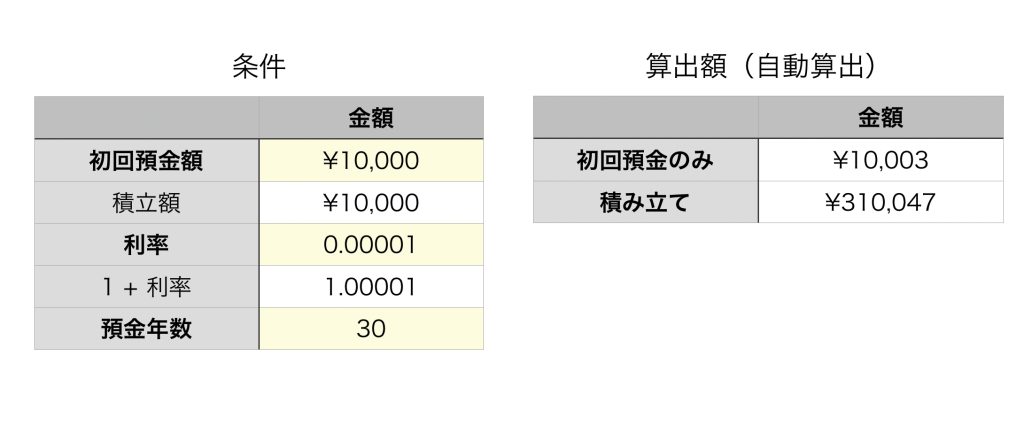
30年後の預金額のシミュレーション

$n$ 年後の残高（元利合計額）の自動算出

Excel・Numbers（表計算ソフト）で30年後の複利の結果をシミュレーションして計算しました！

もう少し簡単なシミュレーションはこちらで紹介しています。

複利シミュレーション（積立額の自動算出）

複利シミュレーション（積立額の自動算出）

複利シミュレーションのテーマ（状況）

A銀行の年利が複利式で「0.001%」でした。
あなたのお年玉を銀行に預けました。
30年後に預金を引き出すとすると、いくらになっているでしょうか？

表計算ソフト

Numbersで解説しますが、ExcelもしくはGoogleスプレッドシートでも同様に作成可能です。

NumbersはiPhoneでもできます！

複利シミュレーションの完成イメージ

次のようなシミュレーションシステムを作ります。

『左側の条件の表（の黄色のトコロ）に必要事項を入力すると、
右側に自動的に未来の預金額が算出できるシステム』です！

今の画面は，次の条件で複利を計算しています；

1万円を預けて30年間寝かすと、３円だけ利子が付く
毎年3万円ずつ積み立てると30年後には31万47円→利子が47円付いた

例えば、預けるのを10万円の定期預金に替えて、利率を0.002%に変更します。

黄色いところだけ変更します。

簡単に30年後の預金額が算出できました♪( ´▽｀)パチパチ

複利シミュレーションの作成手順

STEP①

Numbersに次のように打ち込んでください。そのまま同じように打ち込みます。

Numbersの機能

なお、Numbersでは図のように同じシートに表を2つ並べることができます。

下の図のようにやってください。

※ExcelやGoogleスプレッドシートではできません。

STEP②

[積立額の金額]のところをクリックします。

「=」を入力します。
「初回預金額の金額の¥10,000」のところをクリックします。
[Enter]を押します。

で、OKです。

STEP③

数式の $b$ に対応する数値を入力します。

[1+利率の金額]のところをクリックします。

「=」を入力します。
「1 + 」と入力します。
「利率の0.00001」のところをクリックします。
[Enter]を押します。

STEP④

預けて寝かすタイプの数式の $a(a+r)^n$ を利用します。

[初回預金の金額]のところをクリックします。

「=」を入力します。
「初回預金額の¥10,000」をクリック
「× (1+」と入力
「利率の0.00001」をクリック
「)^」と入力
「預金年数の30」をクリック
[Enter]を押します。

STEP⑤

積立タイプの場合の $\displaystyle \frac{a(b^n-1)}{b-1}$ を利用します。

[積み立ての金額]のところをクリックします。

「=」を入力します。
「初回預金額の¥10,000」をクリック
「× (」と入力
「1+利率の1.00001」をクリック
「)^(」と入力
「預金年数の30」をクリック
「+1) - 1)/」と入力　※「÷」の記号は「/」スラッシュ
「利率の0.00001」をクリック
[Enter]を押します。

で、OKです。

あとは、黄色の数値を自分のシミュレーションしたい値に換えて楽しんでみてください！( ◠‿◠ )

残高（元利合計額）の推移グラフ

Excel・Numbers（表計算ソフト）で30年後の複利の結果をシミュレーションして計算しました！

もう少し数学の計算を踏まえたシミュレーションはこちらで紹介しています。

複利シミュレーション（推移グラフ）