メルカトル図法について

まとめノート
メルカトル図法の常識
地図と経度と緯度の関係
- 地球上の地点 $S(u, v)$ の表現
- メルカトル射影
地図作りの例を計算してみよう

まとめノート

「メルカトル図法」とは

コンパスを基準にして一定方向に進む経路が、直線で表現される地図のこと。

準備

$x \in ( -\pi/2, \ \pi/2)$ について, 次を逆グーデルマン関数と呼ぶ:

$\mathrm{gd}^{-1}(x)=\mathrm{arsinh}\circ \tan(x)$

A. メルカトル射影（定義）

地球上の経度 $u$, 緯度 $v$ の地点 $\mathsf{S}(u,v)$ を, 平面上の次の点に写す.

$\mathsf{Mer}: \mathsf{S}(u,v) \mapsto (u, \mathrm{gd}^{-1}(v))$

微分

地表の点 $\mathsf{S}(u_0,v_0)$ の接平面 $T_{(u_0, v_0)} \mathsf{S}$ における基底 $\mathbf{e}_u$ と $\mathbf{e}_v$ に関するメルカトル射影 $ \mathsf{Mer}$ のヤコビ行列は次の通り:

$J_{\mathsf{Mer}}(u_0, v_0) =
\left[\begin{array}{cc}
1 & 0 \\
0 & \sec v_0
\end{array} \right]$

B. メルカトル射影の等角性

メルカトル射影 $\mathsf{Mer}$ は等角写像である.

C. メルカトル図法の等角性

メルカトル図法では, 経線と緯線がそれぞれ平行なので, メルカトル射影 $\mathsf{Mer}$ の等角性から, 等角航路が直線で表現される.

ポイント解説

$\mathrm{arsinh}(x) = \log(x + \sqrt{x^2+1})$

半径を $1$ とした地球で, 経度が $u$(rad), 緯度が $v$(rad)の地点の座標 $\mathsf{S}(u,v)$ は,

$( \cos u \cos v, \ \sin u \cos v, \ \ \sin v )$.

A

メルカトル射影の縮尺イメージ:

B

接平面の標準的な基底は次の通り:

$\left\{ \begin{array}{l}
\mathbf{e}_u = (-\sin u_0 \cos v_0,\cos u_0 \cos v_0, 0) \\
\mathbf{e}_v = (-\cos u_0 \sin v_0, -\sin u_0 \sin v_0, \cos v_0)
\end{array} \right. $

任意の接ベクトル $a_1 \mathbf{e}_u + a_2 \mathbf{e}_v$ と $b_1 \mathbf{e}_u + b_2 \mathbf{e}_v$ の角度と, $J_{\mathsf{Mer}}(u_0,v_0) \left[\begin{array}{c}
a_1 \\
a_2
\end{array} \right]$ と $J_{\mathsf{Mer}}(u_0,v_0) \left[\begin{array}{c}
b_1 \\
b_2
\end{array} \right]$ の角度が常に等しいものが等角写像である.

常識

地図で作り方で有名なメルカトル図法のメリット・デメリットと、歴史を調べてみました。

メルカトル図法の常識

メルカトル図法の常識

メルカトル図法の採用

メリット

経線はそれぞれ等間隔かつ平行に描かれる
緯線もそれぞれ平行に表現される
地図上の2点を結んだ線が等角航路となる（進行方向が分かりやすい）

※等角航路とは、経線に対して一定の角度を保って進行する経路です。

デメリット

地図上の直線だと最短距離より遠回りになる
地球上で高緯度の距離や面積について，地図上では拡大されて描かれる

メルカトル図法の歴史

歴史の始まり

海図・航路用地図として使われてきた。

1511年

天文学者エアハルト・エッツラウプ（🇩🇪）が作成した地図には，すでに仕組みはあった。

1569年

地理学者ゲラルドゥス・メルカトル（🇧🇪）がドイツで発表した地図にこの投影法があった。

1821年

伊能忠敬（🇯🇵）が，大日本沿海輿地全図を完成させた。

堀田仁助（🇯🇵）は、伊能忠敬が蝦夷地の測量をするにあたって、必要な業績を残している。

現在①

ユニバーサル横メルカトル図法が国際的に利用されている。

日本では国土地理院が発行する地図に利用されている。

現在②

Google Mapsにメルカトル図法が利用されている。

今を生きる

なぜ，Google Mapsは，メルカトル図法を採用したのかな？

常識のまとめ

等角航路

コンパスのN極の方向が経線方向なので、この方向に垂直な方向が緯線方向です。

16世紀の航路では（おそらく）コンパスで進路を決めていたと思われます。

コンパスを基準にして、進む方向を正確に定める基準が「等角航路」で、これを実現した地図が「メルカトル図法」です。

今回の話題は以上です。ありがとうございました。

参考文献

メルカトル図法，Wikipedia，https://ja.m.wikipedia.org/wiki/メルカトル図法
世界地図，総務省統計局，https://www.stat.go.jp/data/sekai/pdf/worldmap.pdf
ユニバーサル横メルカトル図法，Wikipedia，https://ja.m.wikipedia.org/wiki/ユニバーサル横メルカトル図法
Erhard_Etzlaub，Wikipedia，https://en.m.wikipedia.org/wiki/Erhard_Etzlaub
ゲラルドゥス・メルカトル，Wikipedia，https://ja.m.wikipedia.org/wiki/ゲラルドゥス・メルカトル
大日本沿海輿地全図，Wikipedia，https://ja.m.wikipedia.org/wiki/大日本沿海輿地全図

数学

メルカトル図法の地図の作り方の数学をちょっと計算してみました。

地図と経度と緯度の関係
- 地球上の地点 $S(u, v)$ の表現
- メルカトル射影
地図作りの例を計算してみよう

地図と経度と緯度の関係

メルカトル図法で地図を作るために、地球上の経度と緯度から、地図上の点を計算する関数を導入します。

地球上の地点 $S(u, v)$ の表現

地球上で経度 $u$, 緯度 $v$ の地点を $S(u, v)$ とします。地球の半径を $1$ とした場合、この地点は次のように表せます。

$$( \cos u \cos v, \ \sin u \cos v, \ \ \sin v )$$

メルカトル射影

逆グーデルマン関数

$ -\pi/2 < x < \pi/2$ について、逆グーデルマン関数と呼ばれる関数を使います。

$$\mathrm{gd}^{-1}(x)=\mathrm{arsinh}\circ \tan(x)$$

ちなみに、$\mathrm{arsinh}(x) = \log(x + \sqrt{x^2+1})$ です。

メルカトル射影

地球上の経度 $u$, 緯度 $v$ の地点 $\mathsf{S}(u,v)$ を、地図上で次の位置 $(X,Y)$ にプロットしたものがメルカトル図法です。

$$(X,Y)= (u, \mathrm{gd}^{-1}(v))$$

地図作りの例を計算してみよう

地球上の東経 $60^{\circ}$（弧度法 $\pi/3$）, 北緯 $45^{\circ}$（弧度法 $\pi/34$ ）の地点（アラル海）は、メルカトル図法の地図でどこにプロットされるのか計算してみましょう。

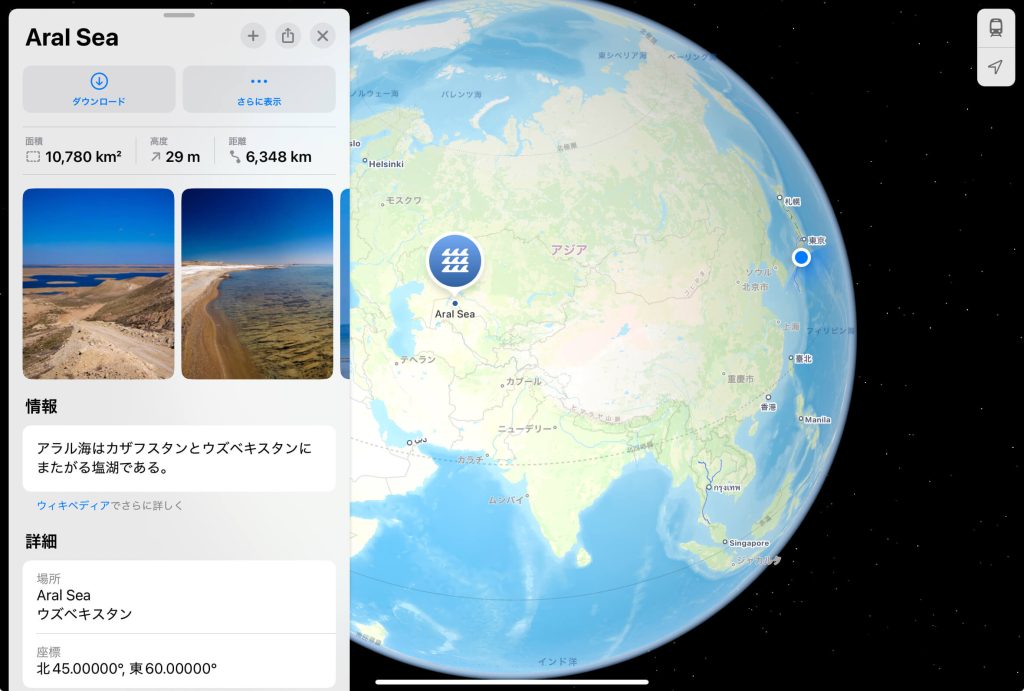
上で述べたとおり、アラル海は地図上の

$$\displaystyle (X,Y) = \left( \frac{\pi}{3}, \ \log(\tan(45^{\circ}) + \sqrt{\tan^2(45^{\circ}) + 1}) \right) = \left( \frac{\pi}{3}, \ \log(1 + \sqrt{2} ) \right)$$

に対応します。実際に計算しましょう。

$$\frac{\pi}{3} = 1.0471 \cdots$$

$$\log(1 + \sqrt{2} ) = 0.0881 \cdots$$

よって、地図上の $(1.047, 0.088)$ の位置にプロットすればOKです。

ちなみに、例えば、地図上で $(X, Y)$ を経度と緯度をそのままにして並べた位置は $(\pi/3, \ \pi/4) \fallingdotseq (1.047, 0.785)$ ですが、メルカトル図法の地図とは異なります。

縦方向の縮尺が異なっているイメージの図を掲載しておきます。

今回紹介した風に地図を作ると、地球上で進行方向を北極方向を基準に測った角度と、地図上で進行方向を経線を基準に測った角度が対応します！

本当に角度が等しくなるのかは、大学の計算が必要なので、ここでは割愛します。

参考文献は次の通りです。

メルカトル図法，Wikipedia，https://ja.m.wikipedia.org/wiki/メルカトル図法
世界地図，総務省統計局，https://www.stat.go.jp/data/sekai/pdf/worldmap.pdf
メルカトル図法の数理ー大学初年次におけるSTEM教材としてー，広島大学，https://home.hiroshima-u.ac.jp/teragai/mercator.pdf
大日本沿海輿地全図，Wikipedia，https://ja.m.wikipedia.org/wiki/大日本沿海輿地全図

まとめノート