• 目次
  • 理解
  • 意味
  • コード
  • まとめ
  • センス

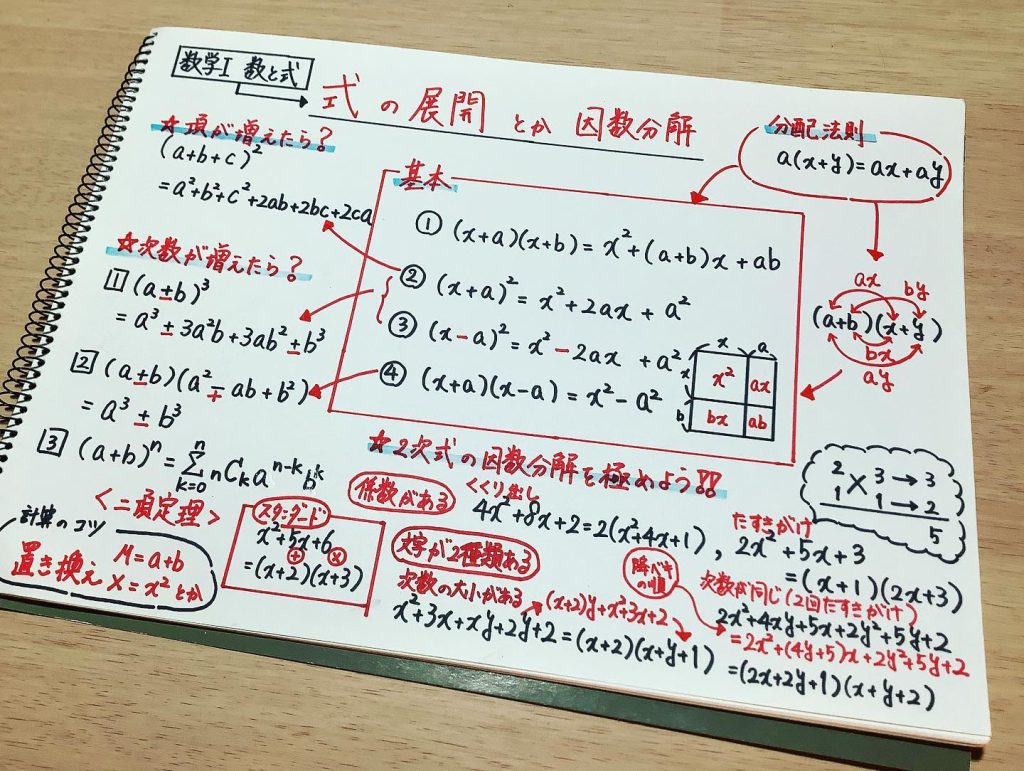
【理解】因数分解とは

共通因数をくくるについて

$ax+ay=a(x+y)$

$ax+bx=(a+b)x$

以下, 展開の式が成り立つので逆方向に計算する.

$a(x+y)$ などの展開の計算方法を習得してみよう。

式の展開公式

$a(x+y) = ax+ay$

$(a+b)x = ax+by$

解説.

数の計算において, 分配法則がいつでも成り立っている.

$$8 \times (10 + 2) = 8 \times 10 + 8\times2.$$

文字式の計算でも同様の分配法則が必ず成り立つものと要請する.

ゆえに, $a(x+y) = ax + ay$ と $(a+b)x = ax+by$ は成り立つものとする.

例えば,

$3(2+4)$ $= 3\times 2 + 3 \times 4$

という計算です。

2次式の因数分解について

$x^2 + (a+b)x + ab=(x+a)(x+b)$

以下, 展開の式が成り立つので逆方向に計算する.

$(x+a)(x+b)$ の展開の計算方法を習得してみよう。

式の展開公式

$(x+a)(x+b) = x^2 + (a+b)x + ab$

解説.

分配法則を利用します.

$a(x+y) = ax + ay$
$(a+b)x = ax + bx$

左辺 $(x+a)(x+b)$ から右辺を導きます.

$$\begin{aligned}
&(x+a)(x+b) \\
&=(x+a)x + (x+a)b \\
&= x^2 + ax + xb + ab \\
&= x^2 + ax + bx + ab\\
&= x^2 + (a+b)x + ab.
\end{aligned}$$

ゆえに, $$(x+a)(x+b) = x^2 + (a+b)x + ab$$ が成立する.

例えば,

$(x+2)(x+3)$ $= x^2 + 5x + 6$

という計算です。

$x^2 + 2ax + a^2=(x+a)^2$

以下, 展開の式が成り立つので逆方向に計算する.

$(x+a)^2$ の展開の計算方法を習得してみよう。

式の展開公式

$(x+a)^2 = x^2 + 2ax + a^2$

解説.

展開の公式を仮定して, 公式を導く.

$(x+a)(x+b) = x^2 + (a+b)x +ab$

左辺 $(x+a)^2$ から, 右辺を導く.

$$\begin{aligned}
&(x + a)^2 \\
&= (x + a)(x + a)\\
&= x^2 + (a+a)x + a\cdot a \\
&= x^2 + 2ax + a^2
\end{aligned}$$

ゆえに, $$(x+a)^2 = x^2 + 2ax + a^2$$ が成立する.

例えば,

$(x+3)^2$ $= x^2 + 6x + 9$

という計算です。

$x^2 - 2ax + a^2=(x-a)^2$

以下, 展開の式が成り立つので逆方向に計算する.

$(x-a)^2$ の展開の計算方法を習得してみよう。

式の展開公式

$(x-a)^2 = x^2 - 2ax + a^2$

解説.

次を仮定して, 公式を導く.

$(x-a)^2 = x^2 + 2ax +a^2$

左辺 $(x-a)^2$ から, 右辺を導く.

$$\begin{aligned}
&(x - a)^2 \\
&= (x + (-a))^2 \\
&= x^2 + \{2 \times (-a)\} x + (-a)^2 \\
&= x^2 - 2ax + a^2
\end{aligned}$$

ゆえに, $$(x-a)^2 = x^2 - 2ax + a^2$$ が成立する.

例えば,

$(x-3)^2$ $= x^2 - 6x + 9$

という計算です。

$x^2 - a^2=(x+a)(x-a)$

以下, 展開の式が成り立つので逆方向に計算する.

$(x+a)(x-a)$ の展開の計算方法を習得してみよう。

式の展開公式

$(x+a)(x-a) = x^2 - a^2$

解説.

次を仮定して, 公式を導く.

$(x+a)(x+b)= x^2 + (a +b)x +ab$

左辺 $(x+a)(x-a)$ から, 右辺を導く.

$$\begin{aligned}
&(x+a)(x-a) \\
&= (x+a)(x+(-a)) \\
&= x^2 + (a + (-a))x + a \cdot (-a) \\
&= x^2 + 0x -a^2\\
&= x^2 -a^2
\end{aligned}$$

ゆえに, $$(x+a)(x-a) = x^2 - a^2$$ が成立する.

例えば,

$(x+3)(x-3)$ $= x^2 - 9$

という計算です。

$acx^2 + (ad+bc)x+bd$ $=(ax+b)(cx+d)$（たすきがけ）

例：$2x^2 + 5xy + 3y^2$ $=(2x+3y)(x+y)$

$$\begin{array}{ccccc}
2x& & 3y& \mathrm{-}&3xy \\
& \times & &&+ \\
x & & y & \mathrm{-} &2xy \\ \hline
2x^2 & & 3y^2 & & 5xy
\end{array}$$

Column. たすきがけを理解する

【たすきがけ】iPadとGoodNotesでたすき掛け難しいを無くす授業

たすき掛けを教えるとき、因数分解をする式の係数の積のパターンを全て検討して、試行錯誤を伝えて、板書に書くこと、生徒のノートに全て書かせることは大変です。 iPadと…

ますレッスン教室

$a^2+b^2+c^2+2ab+2bc+2ca=(a+b+c)^2$

以下, 展開の式が成り立つので逆方向に計算する.

$(a+b+c)^2$ の展開の公式を習得してみよう。

式の展開公式

$(a+b+c)^2$ $= a^2 + b^2 + c^2 + 2ab + 2bc + 2ca$

解説. 置き換えを利用する

$M= a+b$ と置く.

$(a+b+c)^2$ $=(M+c)^2$ $=M^2 + 2Mc + c^2.$

文字に置いた箇所を元に戻すと,

$(a+b)^2 + 2(a+b)c + c^2$

$=a^2$ $+2ab$ $+b^2$ $+2ac$ $+2bc$ $+c^2$

$=a^2$ $+b^2$ $+c^2$ $+2ab$ $+2bc$ $+2ac$.

となる。

ゆえに,

$(a+b+c)^2$ $= a^2 + b^2 + c^2 + 2ab + 2bc + 2ca$

が成立する.

例えば,

$(x+y+1)^2$

$= x^2$ $+ y^2$ $+ 2xy$ $+ 2x$ $+2y$ $+1$

です。

3次式の因数分解について

$x^3 + 3ax^2+3a^2x+a^3=(x+a)^3$

以下, 展開の式が成り立つので逆方向に計算する.

$(x+a)^3$ の展開の公式を習得してみよう。

式の展開公式

$(x+a)^3$ $= x^3 + 3ax^2 + 3a^2x + a^3$

証明.

$(x+a)^3$ を $(x+a)(x+a)^2$ として実際に展開して計算する.

$\begin{aligned}
&(x+a)^3 \\
&\phantom{aa}=(x+a)(x+a)^2 \\
&\phantom{aa}=(x+a)(x^2+2ax + a^2) \\
&\phantom{aa}=x^3+2ax^2 + a^2x \\
&\phantom{aaaaaaa}+ax^2+2a^2x + a^3 \\
&\phantom{aa} = x^3 + 3ax^2 + 3a^2x + a^3
\end{aligned}$

ゆえに,

$(x+a)^3$ $= x^3 + 3ax^2 + 3a^2x + a^3$

が成立する.

例えば,

$(x+2)^3$ $= x^3$ $+ 6x^2$ $+ 12x$ $+ 8$

です。

$x^3 - 3ax^2+3a^2x-a^3=(x-a)^3$

以下, 展開の式が成り立つので逆方向に計算する.

$(x-a)^3$ の展開の公式を習得してみよう。

式の展開公式

$(x-a)^3$ $= x^3 - 3ax^2 + 3a^2x - a^3$

証明.

$(x+a)^3$ の展開公式を利用する.

$(x+a)^3$ $= x^3 + 3ax^2 + 3a^2x + a^3$

$\begin{aligned}
&(x+(-a))^3 \\
&\phantom{a}=x^3 + 3(-a)x^2 + 3(-a)^2x + (-a)^3 \\
&\phantom{a}=x^3 - 3ax^2 + 3a^2x - a^3
\end{aligned}$

ゆえに,

$(x-a)^3$ $= x^3 - 3ax^2 + 3a^2x - a^3$

が成立する.

例えば,

$(x-2)^3$ $= x^3$ $- 6x^2$ $+ 12x$ $- 8$

です。

$x^3 + a^3=(x+a)(x^2-ax+a^2)$

以下, 展開の式が成り立つので逆方向に計算する.

$(x+a)(x^2-ax+a^2)$ の展開の公式を習得してみよう。

式の展開公式

$(x+a)(x^2-ax+a^2)$ $= x^3 + a^3$

証明.

$(x+a)(x^2-ax+a^2)$ を実際に展開して計算する.

$\begin{aligned}
&(x+a)(x^2-ax+a^2) \\
&\phantom{aa}=x^3-ax^2 + a^2x \\
&\phantom{aaaaaa}+ax^2-a^2x + a^3 \\
&\phantom{aa} = x^3 + a^3
\end{aligned}$

ゆえに,

$(x+a)(x^2-ax+a^2)$ $= x^3 + a^3$

が成立する.

例えば,

$(x+1)(x^2-x+1)$

$= x^3$ $+1$

です。

$x^3 - a^3=(x-a)(x^2+ax+a^2)$

以下, 展開の式が成り立つので逆方向に計算する.

$(x-a)(x^2+ax+a^2)$ の展開の公式を習得してみよう。

式の展開公式

$(x-a)(x^2+ax+a^2)$ $= x^3 - a^3$

証明.

$(x-a)(x^2+ax+a^2)$ を実際に展開して計算する.

$\begin{aligned}
&(x-a)(x^2+ax+a^2) \\
&\phantom{aa}=x^3+ax^2 + a^2x \\
&\phantom{aaaaaa}-ax^2-a^2x - a^3 \\
&\phantom{aa} = x^3 - a^3
\end{aligned}$

ゆえに,

$(x-a)(x^2+ax+a^2)$ $= x^3 - a^3$

が成立する.

例えば,

$(x-1)(x^2+x+1)$

$= x^3$ $-1$

です。

$x^3 +y^3 +z^3 -3xyz$ $=(x+y+z)(x^2+y^2+z^2 -xy-yz-zx)$

右辺を展開することで示すことができる.

4次式の因数分解について

$x^4 + a^4$ $=(x^2 +a^2 -\sqrt{2}xa)(x^2 +a^2 +\sqrt{2}xa)$

$x^4 + a^4$
$=x^4+2x^2a^2+a^4-2x^2a^2$
$=(x^2 +a^2)^2 -2x^2a^2$
$=(x^2 +a^2 -\sqrt{2}xa)(x^2 +a^2 +\sqrt{2}xa)$

$x^4 - a^4$ $=(x^2 + a^2)(x + a)(x-a)$

$x^4 - a^4$
$=(x^2 + a^2)(x^2 - a^2)$
$=(x^2 + a^2)(x + a)(x-a)$

$n$ 次式の因数分解について

$x^n - y^n$ $= (x - y)(x^{n-1} + x^{n-2}y + \cdots + x y^{n-2} + y^{n-1})$

以下, 展開の式が成り立つので逆方向に計算する.

$(x-y)$ $(x^{n-1}$ $+x^{n-2}y$ $+ \cdots$ $+xy^{n-2} $ $+y^{n-1})$ の展開の公式を習得してみよう。

式の展開公式

$(x-y)$ $(x^{n-1}$ $+x^{n-2}y$ $+ \cdots$ $+xy^{n-2}$ $+y^{n-1})$ $= x^n - y^n$

証明.

$(x-y)$ $(x^{n-1}$ $+x^{n-2}y$ $+ \cdots$ $+xy^{n-2} $ $+y^{n-1})$ について, $x-y$ を $x$ と $-y$ に分割して, それぞれ展開して和を計算する.

$x$ と $x^{n-1}$ $+x^{n-2}y$ $+ \cdots$ $+xy^{n-2}$ $+y^{n-1}$ の積は

$x^n+x^{n-1}y + \cdots +x^2y^{n-2} +xy^{n-1}$

である.

$-y$ と $x^{n-1}$ $+x^{n-2}y$ $+ \cdots$ $+xy^{n-2}$ $+y^{n-1}$ の積は

$-x^{n-1}y - \cdots -x^2y^{n-2} -xy^{n-1} -y^{n}$

である.

これらの和は $x^n - y^n$ である.

ゆえに,

$(x-y)$ $(x^{n-1}$ $+x^{n-2}y$ $+ \cdots$ $+xy^{n-2}$ $+y^{n-1})$

が成立する.

例えば,

$(x-1)$ $(x^3$ $+x^2$ $+x$ $+1)$

$= x^4$ $+1$

です。

$x^n + y^n$ $= (x + y)(x^{n-1} - x^{n-2}y + \cdots - x y^{n-2} + y^{n-1})$ ($n$ は奇数)

以下, 展開の式が成り立つので逆方向に計算する.

$(x+y)$ $(x^{n-1}$ $-x^{n-2}y$ $+ \cdots$ $-xy^{n-2} $ $+y^{n-1})$ の展開の公式（ $n$ が奇数のときのみ）を習得してみよう。

式の展開公式

$(x+y)$ $(x^{n-1}$ $-x^{n-2}y$ $+ \cdots$ $-xy^{n-2}$ $+y^{n-1})$ $= x^n + y^n$

ただし, $n$ は奇数とする.

※ $n$ が偶数の場合は $x^{n-1}$, $x^{n-2}y$, $\cdots$, $xy^{n-2}$, $y^{n-1}$ の係数が正負交互であると $y^{n-1}$ の係数を正にすることができない. $n$ が奇数のときのみ今回の式が定義できる.

証明.

$(x+y)$ $(x^{n-1}$ $-x^{n-2}y$ $+ \cdots$ $-xy^{n-2}$ $+y^{n-1})$ について, $x+y$ を $x$ と $y$ に分割して, それぞれ展開して和を計算する.

$x$ と $x^{n-1}$ $-x^{n-2}y$ $+ \cdots$ $-xy^{n-2}$ $+y^{n-1}$ の積は

$x^n-x^{n-1}y + \cdots -x^2y^{n-2} +xy^{n-1}$

である.

$y$ と $x^{n-1}$ $-x^{n-2}y$ $+ \cdots$ $-xy^{n-2}$ $+y^{n-1}$ の積は

$x^{n-1}y + \cdots +x^2y^{n-2} -xy^{n-1} +y^{n}$

である.

これらの和は $x^n + y^n$ である.

ゆえに,

$(x+y)$ $(x^{n-1}$ $-x^{n-2}y$ $+ \cdots$ $-xy^{n-2}$ $+y^{n-1})$ $= x^n + y^n$

が成立する.

例えば,

$(x+1)$ $(x^4$ $-x^3$ $+x^2$ $-x$ $+1)$

$= x^5$ $+1$

です。

除法を利用して因数分解する

$A(x)$ が $P(x)$ で割り切れ, この商が $Q(x)$ であるとき, $A(x) = P(x)Q(x)$ と因数分解できる.

【意味】因数分解の意味

【遊び】折り紙で因数分解

折り紙で2次式の因数分解の図形的説明

2次式の因数分解を折り紙（オリガミ）で体験します。

式の因数分解の図形的な意味も理解できます！

因数分解の図形的意味を折り紙で表現する

単項式 $x^2$ と $y^2$, $xy$ を折り紙で作る

$x^2$ と $y^2$ を作る

$xy$ を作る

「たすきがけ」と折り紙

$2x^2 +5xy +3y^2$ の図形的な意味

因数分解の式 $(x+y)(2x+3y)$ の意味

「たすき」は使っていないので、ただの因数分解です。

「共通因数のくくりだし」と折り紙

$4x^2 +8xy +4y^2$ の図形的な意味

この折り紙を「同じサイズの正方形に分ける」ことをしてみよう。

因数分解の式 $4(x+y)^2$ の意味

1つの正方形を作った
2つの長方形を作った
4つの正方形を作った

「次数に着目して因数分解」と折り紙

$x^2 +3x +xy +2y +2$ の図形的な意味

因数分解の式 $(x+y+1)(x+2)$ の意味

長さ $x$ で合わせると上手くいかなかった
長さ $y$ で合わせて1つの長方形を作った

「2回たすきがけする」と折り紙

$2x^2 +4xy +5x+2y^2+5y +2$ の図形的な意味

因数分解の式 $(2x+2y+1)(x+y+2)$ の意味

以上です！

折り紙で2次式の展開！【式の展開の図形的意味】

2次式の展開を折り紙（オリガミ）で体験します。 式の展開の図形的な意味も理解できます！ 2次式の展開の図形的意味を折り紙で表現する 分配法則と折り紙 $a(x+y)=ax+ay$ …

ますレッスン教室
折り紙で3次式の展開と因数分解【図形的意味】

3次式の展開と因数分解を折り紙（オリガミ）で体験します。 式の展開と因数分解の図形的な意味も理解できます！ 3次式の展開と因数分解の図形的意味を折り紙で表現する $x…

ますレッスン教室
折り紙で平方完成！【図形的説明】

平方完成を折り紙（オリガミ）で体験します。 平方完成の図形的な意味も理解できます！ 平方完成と折り紙 $x^2 +3x$ の平方完成の折り紙 $x^2 +3x$ を折り紙で用意する $\…

ますレッスン教室

折り紙で3次式の因数分解の図形的説明

3次式の展開と因数分解を折り紙（オリガミ）で体験します。

式の展開と因数分解の図形的な意味も理解できます！

3次式の展開と因数分解の図形的意味を折り紙で表現する

$x^3 +2x^2 +x$ $=x(x+1)^2$ の折り紙

$x^3 +2x^2 +x$ の図形的な意味

因数分解 $x(x+1)^2$ の意味

$x^3+3ax^2+3a^2x+a^3$ $=(x+a)^3$ の折り紙

$x^3+3ax^2+3a^2x+a^3$ の図形的な意味

因数分解 $(x+a)^3$ の意味

現在は、ここまで。

折り紙で2次式の展開！【式の展開の図形的意味】

2次式の展開を折り紙（オリガミ）で体験します。 式の展開の図形的な意味も理解できます！ 2次式の展開の図形的意味を折り紙で表現する 分配法則と折り紙 $a(x+y)=ax+ay$ …

ますレッスン教室
折り紙で2次式の因数分解！【因数分解の図形的意味】

2次式の因数分解を折り紙（オリガミ）で体験します。 式の因数分解の図形的な意味も理解できます！ 因数分解の図形的意味を折り紙で表現する 単項式 $x^2$ と $y^2$, $xy$…

ますレッスン教室
折り紙で平方完成！【図形的説明】

平方完成を折り紙（オリガミ）で体験します。 平方完成の図形的な意味も理解できます！ 平方完成と折り紙 $x^2 +3x$ の平方完成の折り紙 $x^2 +3x$ を折り紙で用意する $\…

ますレッスン教室

なんで因数分解するのか

【数学を応用する】なんで因数分解を勉強するの？→使わない

因数分解なんて、大人になってから使わないよ。 因数分解なんて、社会で使わないよ。と多く耳にします。 すなわち「因数分解意味分からん」ともよく聞きます。 この質問に…

ますレッスン教室

【コード】Pythonで因数分解

四則演算（加減乗除）とべき乗 $a^b$ の計算方法

四則演算（加減乗除）とべき乗をPythonで計算してみよう。

演算

足し算は+を使う。引き算は-を使う。掛け算は*を使う。割り算は/を使う。べき乗は**を使う。

Python. $a+b$, $a-b$, $a \times b$, $a \div b$, $a^b$ を計算する。

a = 3
b = 2

print(a + b) #足し算
print(a - b) #引き算
print(a * b) #掛け算
print(a / b) #割り算
print(a ** b) #べき乗

5
1
6
1.5
9

factor()による式の展開

式の因数分解をPythonで計算してみよう。

因数分解

文字式を扱うためにsympyモジュールを利用する。

factor()関数で式を因数分解する。

Python. $2x^2+5xy+3y^2$ を因数分解する。

import sympy

#xとyを文字として定義する
x = sympy.Symbol('x')
y = sympy.Symbol('y')

#多項式Qを定義する
Q = 2*x**2 + 5*x*y + 3*y**2

#Qを展開して表示する
print(sympy.factor(Q))

#QをLaTeX表示する
display(sympy.factor(Q))

まとめノート

「因数分解」とは

式の展開の逆の計算で、式を次数のより低い式の積で表すこと。

共通因数でくくる

$Ax + Ay = A(x+y)$

A. 2次式の因数分解（公式）

  1. $x^2 + (a+b)x + ab$ $= (x+a)(x+b)$
  2. $x^2 + 2ax + a^2= (x + a)^2$, $x^2 - 2ax + a^2= (x - a)^2$
  3. $x^2 - a^2$ $= (x+a)(x-a)$

B. 3次式の因数分解（公式）

  1. $x^3 + 3ax^2 + 3a^2x+ a^3 = (x + a)^3$, $x^3 - 3ax^2 + 3a^2x - a^3 = (x - a)^3$
  2. $x^3 + a^3= (x + a)(x^2 - ax + a^2)$, $x^3 - a^3= (x - a)(x^2 + ax + a^2)$
  3. $a^3 + b^3 + c^3 - 3abc$ $=(a+b+c)(a^2 + b^2 + c^2 - ab-bc-ca)$

除法

$P(x) \div A(x) = Q(x)$ $\Rightarrow$

$P(x) = A(x)Q(x)$

(因数分解)

C. $n$次式の因数分解（公式）

  1. $x^n + {}_n\mathrm{C}_1 x^{n-1}a + \cdots + {}_n\mathrm{C}_{n-1}xa^{n-1} + a^n$ $= (x+a)^n$
  2. $x^n - a^n$ $= (x - a)(x^{n-1} + x^{n-2}a + \cdots + x a^{n-2} + a^{n-1})$

ポイント解説

係数を簡単にする

ために共通因数をくくることもある。

A

長方形の縦と横の辺の長さを求める意味をもつ。

たすきがけ

計算例；$2x^2 + 5xy + 3y^2$ $=(2x+3y)(x+y)$

$$\begin{array}{ccccc}
2x& & 3y& \mathrm{-}&3xy \\
& \times & &&+ \\
x & & y & \mathrm{-} &2xy \\ \hline
2x^2 & & 3y^2 & & 5xy
\end{array}$$

除法

多項式 $P(x)$ が $A(x)$ で割り切れ, 商が $Q(x)$ という意味である.

因数定理

多項式 $P(x)$ と複素数 $\alpha$ について,

$P(\alpha) = 0$

ならば

$P(x)$ は $x - \alpha$ を因数

にもつ。

発展

任意の多項式は少なくとも1つの複素数根を持つ（代数学の基本定理）。

モチベーション

動画のチェック

$x^2 + 6x + 5$ を因数分解すると？

$(x+2)(x+3)$

残念！

問題の式は動画の中の式とは違うよ！

$(x+1)(x+5)$

正解！

おめでとう！

パチパチ！

$(x+2)(x+4)$

ざんねん！

$x^2 + 6x + 8$ という式だったら、この答えだよ！

$(x+1)(x+4)$

ざんねん！

$x^2 +56x + 4$ という式だったら、この答えだよ！

関連知識のリンク

カテゴリー
絵馬
タグ

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

前の記事
式の展開について
2024-03-26
次の記事
実数・数直線について
2024-03-26