- 表紙
- まとめ
- ①自然
- ②イメージ
- ③理解
- ④コード
数学のまとめ
「楕円」とは
円周を一定方向に伸縮してできる曲線のこと。
定義
２点からの距離の和が一定の点の軌跡を楕円という.
数式
距離の和を $2a$, 焦点を $\mathrm{F}$ と $\mathrm{F}'$, 動点を $\mathrm{P}$ とすると, $\mathrm{PF} + \mathrm{PF'} = 2a$ である.
A. 楕円の方程式
中心が原点で, 横半径 $a$, 縦半径 $b$ のとき, $\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ は楕円を描く.
焦点
$b<a$ のとき, 焦点の座標を $\pm(c,0)$ とすると, $c^2 = a^2 - b^2$ が成り立つ.
B. 楕円の離心率
楕円の離心率 $e$ は次で得られる: $\displaystyle e = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a}$
C. 楕円の接線の方程式
楕円上の $(x_0, y_0)$ を通る接線の方程式は次で得られる: $\displaystyle \frac{x_0}{a^2}x + \frac{y_0}{b^2}y = 1$
ポイント解説
イメージ
楕円は自然の造形でも作られます。
A
横方向に長い楕円になります。
$a < b$ のときは, 焦点 $(0, c)$, $(0, -c)$ の縦方向に長い楕円です. ($c^2 = b^2 - a^2$)
B
楕円の離心率は, 焦点間の距離と長軸の長さの比で求まります。なお, $0 < e <1$ です。
自然がつくる楕円
塩山
穴を開けた円板に塩を降り積もらせると、楕円ができる。
円錐切断
楕円の直感的イメージ
円を伸縮させて楕円をつくろう！
円を伸縮させた形
主張
問い
円を伸縮させたら、楕円になるらしい。
楕円の方程式
単位円 $x^2 + y^2 =1$ を $x$ 軸方向に $a$ 倍，$y$ 軸方向に $b$ 倍した図形の方程式は次と一致する：
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
確かめ
【1】基本の円を用意する
単位円 $x^2 + y^2 = 1$ を用意する。
単位円とは中心が原点 $(0,0)$, 半径が 1 の円です。
【2】横方向に伸縮させる
円を 「$x$ 軸方向に伸縮させる」ことを，$y$軸を基準に同じ比率（$a>0$）で等倍すると定める。
つまり，円周上の点 $(x,y)$ を $(ax, y)$ と変形する。等倍されたあとの円周上の点の座標は、$(ax, y)$ となる。
【3】縦方向に伸縮する
円を 「$y$ 軸方向に伸縮させる」ことを，$x$軸を基準に同じ比率（$b>0$）で等倍すると定める。
つまり，円周上の点 $(x,y)$ を $(x, by)$ と変形する。等倍されたあとの円周上の点の座標は、$(x, by)$ となる。
【4】伸縮後の座標と方程式
円を $x$軸と$y$軸方向にそれぞれ伸縮したあとの点$(X,Y)$ の座標は $(ax, by)$ である。
$$(X,Y) = (ax, by)$$
$x = X/a$ と $y = Y/b$ を，単位円の方程式（ $x^2 + y^2 = 1$ ）に代入すると，楕円の方程式を得る。
$$\displaystyle \left( \frac{X}{a} \right)^2 + \left( \frac{Y}{b} \right)^2 = 1$$
イメージにピッタリだね！
楕円の数式
数学的には、2点からの距離の和が一定の点の軌跡として与えられます。
楕円の基礎
数式①
楕円の中心を原点，２つの焦点を $x$軸上に取ったときの楕円の方程式は，次の通りである：
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
このとき，定数 $a$ は，楕円の横軸方向の半径であり，定数 $b$ は，楕円の縦軸方向の半径である。
楕円の長軸と短軸
$a > b$ のとき、横方向に長い楕円になります。
- 長軸半径 $a$，短軸半径 $b$
- 焦点：$(\sqrt{a^2 - b^2}, 0), \ (-\sqrt{a^2 - b^2}, 0)$
- 離心率：$\displaystyle e = \frac{\sqrt{a^2 - b^2}}{a} < 1$
$a < b$ のとき、縦方向に長い楕円になります。
- 短軸半径 $a$，長軸半径 $b$
- 焦点：$(0, \sqrt{b^2 - a^2}), \ (0, -\sqrt{b^2 - a^2})$
- 離心率：$\displaystyle e = \frac{\sqrt{b^2 - a^2}}{b} < 1$
$a=b=1$ のときは真ん丸な「円」だよ。
媒介変数表示（楕円）.
$$\displaystyle (x, \ y) = (a \cos \theta, \ \ b \sin \theta )$$
楕円の数式の成り立ち
$a > b$ のときの楕円の方程式を定義から構築します。
焦点FとF'からの距離の和が $2a$ である点Pの軌跡が楕円である。
$$\displaystyle \mathrm{PF} + \mathrm{PF'} = 2a$$
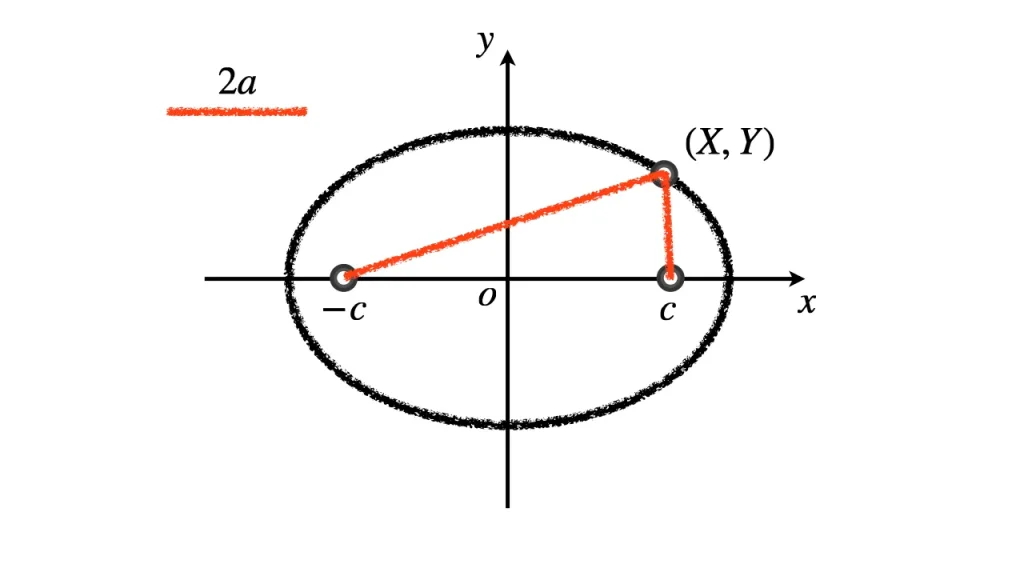
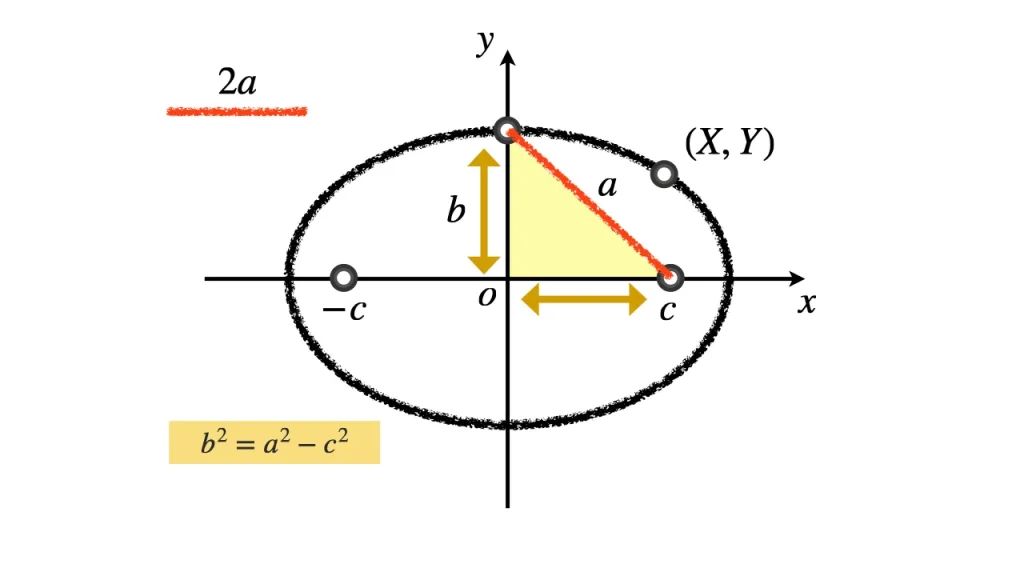
焦点の座標を $\mathrm{F}(c, 0), \ \mathrm{F'}(-c, 0)$ とする。
点Pの座標を $(x,y)$ とする。
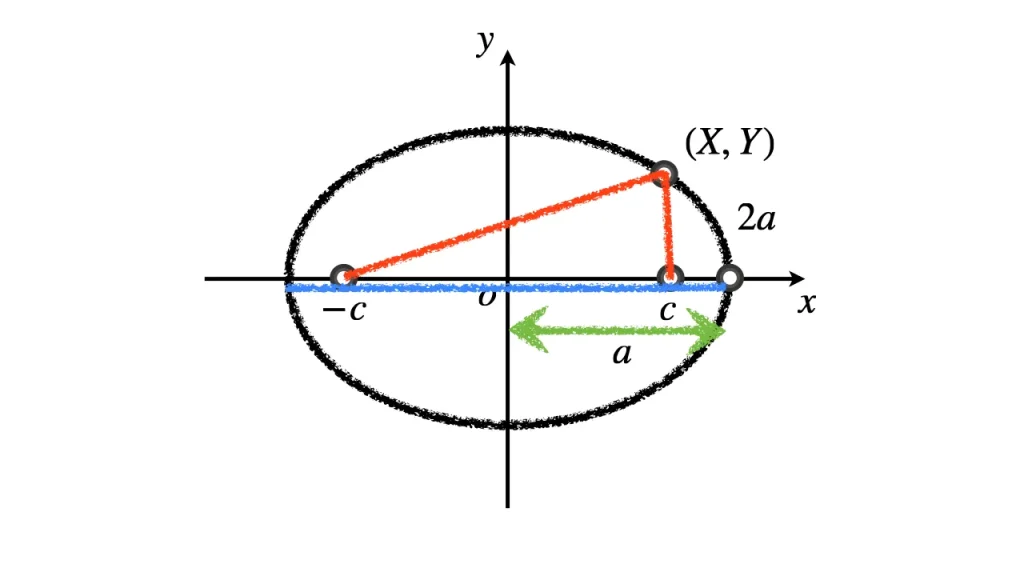
図から，$a$ が楕円の長軸方向の半径の長さと一致することが分かる。
$\displaystyle \mathrm{PF} = \sqrt{(x-c)^2 + y^2}$
$\displaystyle \mathrm{PF'} = \sqrt{(x-(-c))^2 + y^2}$
これらを楕円の定義式に代入すると，次を得る：
$$\sqrt{(x-c)^2 + y^2} + \sqrt{(x-(-c))^2 + y^2} = 2a$$
$\sqrt{(x-c)^2 + y^2} + \sqrt{(x-(-c))^2 + y^2} = 2a$
$\Rightarrow$ $\sqrt{(x-c)^2 + y^2} = 2a - \sqrt{(x-(-c))^2 + y^2}$
$\Rightarrow$ $(x-c)^2 + y^2 = 4a^2 - 4a \sqrt{(x+c)^2 + y^2} + (x+c)^2 + y^2$
$\Rightarrow$ $a \sqrt{(x+c)^2 + y^2} = a^2 + cx$
$\Rightarrow$ $(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$
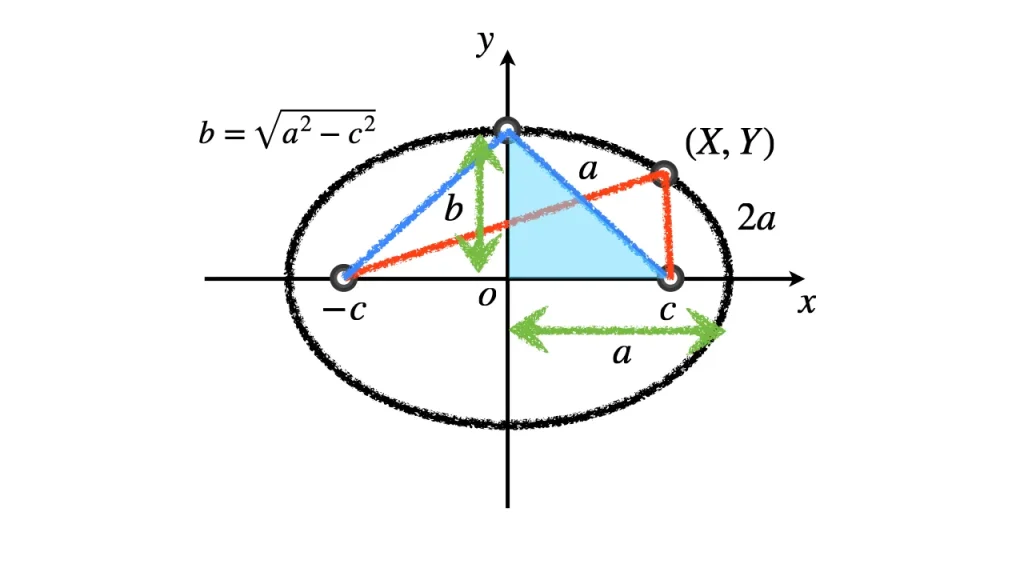
$a^2 - c^2$ は，図より短軸半径の $b^2$ と一致する。
$\Rightarrow$ $(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$
$\Rightarrow$ $b^2 x^2 + a^2y^2 = a^2b^2$
$$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
ただし，$c^2 = a^2 + b^2$ である。■
楕円のPythonコード
半径から楕円を導く
import matplotlib.pyplot as plt
import numpy as np
# 長軸と短軸の長さ
a = 2
b = 1
# パラメータを生成
theta = np.linspace(0, 2 * np.pi, 1000)
# 楕円の座標計算
x = a * np.cos(theta)
y = b * np.sin(theta)
# 楕円を描画
plt.plot(x, y, label=f'Major Axis = {a}, Minor Axis = {b}')
plt.title('Ellipse with Given Major and Minor Axes')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True)
plt.show()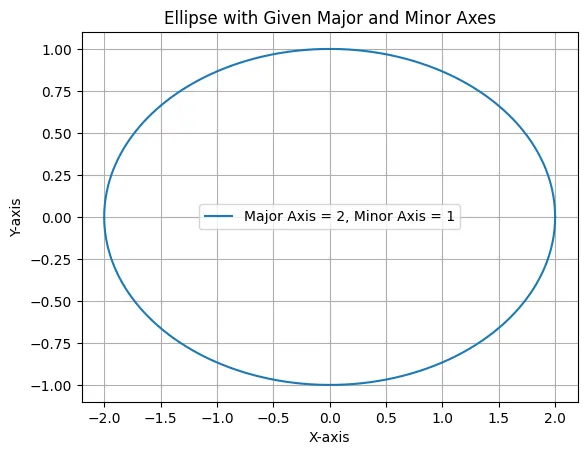
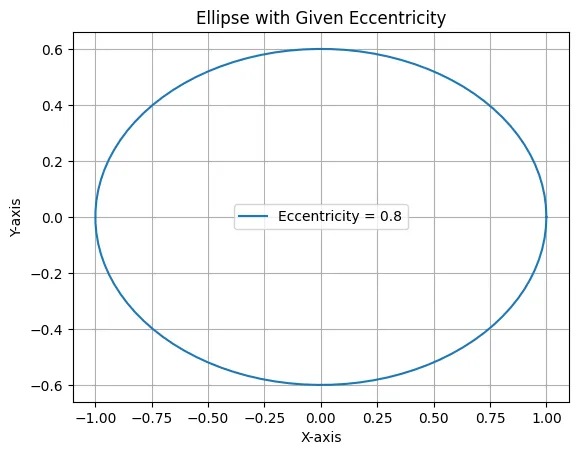
離心率から楕円を導く
import matplotlib.pyplot as plt
import numpy as np
# 離心率
eccentricity = 0.8
# 楕円のパラメータ
a = 1 # 長軸の半径
b = a * np.sqrt(1 - eccentricity**2) # 短軸の半径
# パラメータを生成
theta = np.linspace(0, 2 * np.pi, 100)
# 楕円の座標計算
x = a * np.cos(theta)
y = b * np.sin(theta)
# 楕円を描画
plt.plot(x, y, label=f'Eccentricity = {eccentricity}')
plt.title('Ellipse with Given Eccentricity')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True)
plt.show()
